Podobnosť trojuholníkov - príklady
Pokyny: Vyriešte každú úlohu starostlivo a ukážte svoje celé riešenie. Ak je to vhodné, vykonajte skúšku správnosti riešenia.Počet nájdených príkladov: 154
- Lichobežník - TST9
Lichobežník ABCD je zložený z piatich trojuholníkov. Body E, G delia úsečku AB v pomere 2:4:3 (v tomto poradí) na tri úsečky. Bod F je stredom úsečky AD. Trojuholník AEF je rovnoramenný a pravouhlý. Trojuholníky GBC a CDG sú pravouhlé. Obsah trojuholníka - Tieň - rozhľadňa
Aká vysoká je rozhľadňa, ak vrhá tieň dlhý 9,6 m presne v rovnakom okamihu, keď polmetrová tyč vrhá tieň dlhý 30 cm. - Podobnosť trojuholníkov
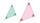Máme podobné trojuholníky ABC s uhlom CAB=45° a uhlom ACB= 30° a podobný trojuholník OPN. Aký je uhol NOP na podobnom trojuholníku? - Vonkajšie uhly
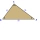V trojuholníku ABC sa veľkosť vonkajšieho uhla pri vrchole C rovná 126°. Veľkosť vnútorných uhlov pri vrcholoch A, B sú v pomere 5: 9. Vypočítaj veľkosť vnútorných uhlov α, β, γ trojuholníka ABC.
- Opísaná kružnica
Vypočítajte polomer kružnice opísaneho trojuholníku, ktorý má rozmery strán 8, 10 a 14cm. - Výška topoľa
Z rozhľadne vysokej 40 m je vidieť vrchol topoľa pod hĺbkovým uhlom o veľkosti 50°10' a pätu topoľa v hĺbkovom uhle o veľkosti 58°. Vypočítajte výšku topoľa. - Vypočítajte 253
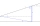Vypočítajte výšku stožiaru, ktorého pätu vidíme v hĺbkovom uhle 11° a vrchol vo výškovom uhle 28°. Stožiar je pozorovaný z miesta 10 m nad úrovňou päty stožiara. - Školská 82470 Školská budova vrhá na rovinu dvora tieň 16 m dlhý av tom istom čase vrhá zvislá metrová tyč tieň 132 cm dlhý. Určite výšku budovy.
- Presypacie
Presýpacie hodiny pozostavajú z dvoch zhodných nádobiek v tvare rotačných kúžeľov. Pre jednoduchosť predpokladame, že kúžele sa dotýkajú iba svojimi vrcholmi. Piesok siaha do polovice výšky spodného kúžeľa. Po preklopení hodií trvá presne 21 minút, kým sa
- Trojuholníku 81499
Vyber trojuholník, ktorý je podobný zadanému trojuholníku. ∆ RTG, r= 24 dm, t = 28 dm, g= 30 dm. - ∆ SHV = 6 dm, h = 7,5 dm, v = 7 dm - ∆ VSH = v = 7 dm, s = 6 dm, h = 7,5 dm - ∆ HVS = h = 7,5 dm, v = 7 dm, s = 6 dm. - ∆ VHS = v = 7 dm, h = 7,5 dm, s = 6 - Trojuholníku 81484
Vyber trojuholník, ktorý je podobný zadanému trojuholníku. - ∆ TFC = t = 8 cm, f = 9 cm, c = 7 cm. : ∆ PKU = p = 45 cm, k = 35 cm, u = 40 cm. ∆ UPK = u = 40 cm, p = 45 cm, k = 35 cm. ∆ PUK = p = 45 cm, u = 40 cm, k = 35 cm. ∆ KPU = k = 35 cm, p = 45 cm, u - Trojuholníky 81480 Rozhodni, či sú trojuholníky podobné. Vyber medzi Áno/Nie. ∆ YUO: y= 9m, u= 17 m, o= 12 m, ∆ ZXV= z= 207 dm, x= 341 dm, v= 394 dm
- Trojuholník 155
Trojuholník ABC a trojuholník ADE sú podobné. Vypočítajte v centimetroch štvorcových obsah trojuholníka ABC, ak dĺžka strany DE je 12 cm, dĺžka strany BC je 16 cm a obsah trojuholníka ADE je 27 cm². - Obvod 56 Obvod trojuholníka MAK je 216 mm, strana a=81 mm a strana k=62 mm. Urč dĺžku strany z trojuholníka OSA, ak platí, že trojuholník MAK je zhodný s trojuholníkom OSA.
- Obsah 41 Obsah pravouhlého trojuholníka KLM s pravým uhlom pri vrchole L je 60 mm štvorcových a jeho odvesna k má dĺžku 10 mm. Trojuholníky KLM a RST sú podobné, pomer podobnosti je k=2,5 . Vypočítaj obsah trojuholníka RST.
- Vypočítaj 376
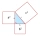Vypočítaj obvod trojuholníka ABC, ak vieš, že je podobný trojuholníku EFG, v ktorom e=144 mm, f=164 mm, g=92 mm a pomer podobnosti je 4. Výsledok vyjadri v cm. - V tábore 2
V tábore robili deti maketu táboriska. V jej strede bol javor ktorý na makete mal výšku 28 cm. Vypočítaj akú výšku má javor v táborisku ak ráno vrhá tieň 14 m dlhý a jeho maketa má vtedy tieň 49 cm dlhý. - Nicolette
Nicolette vyrába malý korálkový náramok z 5 červených korálok, 8 fialových korálok a 6 zelených korálok. Veľký náhrdelník má rovnaký pomer korálok ako malý náramok. Ak veľký náhrdelník vyžaduje 15 červených guľôčok, koľko fialových guľôčok je potrebných n - Trojuholníky 76704
Nájdite všetky pravouhlé trojuholníky, ktorých dĺžky strán tvoria aritmetickú postupnosť.
Aký dlhý je tieň stromu vysokého 7,6m ak tieň 190cm vysokej dopravnej značky je dlhý 3,3m?Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať. Riešenie príkladov z matematiky.
