Vzdialenosť bodov 2

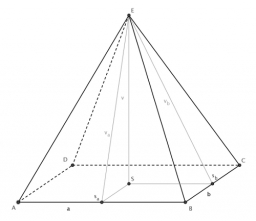
Je daný pravidelný štvorboký ihlan ABCDV, v ktorom AB= a= 4 cm a v= 8 cm. Nech S je stred CV. Vypočítajte vzdialenosť bodov A a S.

Správny výsledok:

x =  5,831 cm

Riešenie:

a=4 cm v=8 cm  u=2⋅ a=2⋅ 4=4 2 cm≐5.6569 cm  s=v2+(u/2)2=82+(5.6569/2)2=6 2 cm≐8.4853 cm s2=s/2=8.4853/2=3 2 cm≐4.2426 cm  ACV=arctan⁡(vu/2)=arctan⁡(85.6569/2)≐1.231 rad  x2=u2+s22−2⋅ u⋅ s2⋅ cos⁡(ACV)  x=u2+s22−2⋅ u⋅ s2⋅ cos⁡(ACV)=5.65692+4.24262−2⋅ 5.6569⋅ 4.2426⋅ cos⁡1.231=34=5.831 cm

Skúsiť iný príklad


Budeme veľmi radi, ak nájdete chybu v príklade, pravopisné chyby alebo nepresnosť a ju nám prosím pošlete. Ďakujeme!






Zobrazujem 0 komentárov:
avatar




Tipy na súvisiace online kalkulačky
Pytagorova veta je základ výpočtov aj kalkulačky pravouhlého trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.

Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:


 
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1   video2

Ďaľšie podobné príklady a úlohy:

  • Uhol mimobežiek
    ihlan Je daný pravidelný štvorboký ihlan ABCDV ; |AB|=4cm; v=6cm. Určte uhol priamok AD a BV.
  • AV-CV
    ihlan V pravidelnom ihlane, v ktorom hrana podstavy je |AB|=4cm; výška=6cm vypočítaj uhol priamok AV a CV, V = vrchol.
  • Štvorboký ihlan 5
    jehlan_4b_obdelnik_1 Daný je pravidelný štvorboký ihlan s podstavou štvorec. Výška telesa je 30 cm a V= 1000cm³. Vypočítaj stranu a a obsah.
  • Hranol 4b
    hranol4sreg Vypočítajte objem a povrch pravidelného štvorbokého hranola ktorého výška je 28,6cm a telesová uhlopriečka zviera s rovinou podstavy uhol 50 stupňov.
  • Ihlan
    jehlan_3 Je daný pravidelný štvorboký ihlan, dĺžka podstavné hrany je 6 cm a výška ihlanu je 10 cm. vypočítajte dĺžku bočnej hrany.
  • Pravidelný
    jehlan_4b_obdelnik_1 Pravidelný štvorboký ihlan má podstavnou hranu a = 1,56 dm a výšku v = 2,05dm. Vypočítajte: a) odchýlku roviny bočnej steny od roviny podstavy b) odchýlku bočnej hrany od roviny podstavy
  • Ihlan ABCDV
    ihlan Ihlan ABCDV má dĺžky hrán: AB=4, AV=7. Aká je jeho výška?
  • V štvorci
    stvorec V štvorci ABCD so stranou a = 6 cm je bod E stred strany AB a bod F stred strany BC. Vypočítajte veľkosť všetkých uhlov trojuholníka DEF a dĺžky jeho strán.
  • Odchýlka priamok
    kvadr_1 Určte odchýlku priamok AG, BH v kvádra ABCDEFGH, ak je dané | AB | = 3cm, | AD | = 2cm, | AE | = 4cm
  • Trojboký ihlan
    3sidesPyramid Je daný kolmý pravidelný trojboký ihlan: a = 5 cm, v = 8 cm, V = 28,8 cm3. Aký je jeho obsah (povrch)?
  • Daný je
    ihlan_2 Daný je pravidelný štvorboký ihlan s postavou štvorec. Strana a=16 cm, S= 736 cm². Vypočítaj h (výšku telesa) a objem telesa V.
  • Pravidelný 4bi
    ihlan_3 Pravidelný štvorboký ihlan má uhlopriečku podstavy 5√2 cm a bočné hrany majú dĺžku 12√2 cm. Vypočítaj výšku ihlana a jeho povrch.
  • Vypočítajte
    kvadr_diagonal Vypočítajte veľkosť odchýlky telesové uhlopriečky a bočné hrany c kvádra s rozmermi: a = 28cm, b = 45cm a c = 73cm. Ďalej vypočítajte veľkosť odchýlky telesové uhlopriečkou od roviny podstavy.
  • Štvorboký ihlan
    ihlany Vypočítajte objem a povrch pravidelného 4bokého ihlanu, ktorého podstavná hrana je dlhá 4 cm. Odchýlka bočných stien od roviny je 60 stupňov.
  • Štvorboký ihlan
    jehlan Je daný pravidelný štvorboký ihlan. Dĺžka hrany podstavy a = 6,5 cm, bočná hrana s = 7,5 cm. Vypočítajte objem a obsah plášťa.
  • Obsah 18
    rt_iso2 Obsah rovnoramenného trojuholníka je 8 cm2, dĺžka jeho ramena je 4 cm. Vypočítajte veľkosti jeho vnútorných uhlov.
  • Ihlan 8
    ihlan Vypočítajte objem a povrch pravidelného štvorbokého ihlanu so stranou podstavy 9 cm, bočná stena zviera s podstavou uhol 75°.