Algebra - príklady

Algebra je odvetvie matematiky, ktoré na riešenie operácií používa nielen čísla a znaky, ale aj písmená. Napríklad 3x+5x je 8x. Čiže práca s výrazmi, riešenie rovníc, sústav rovníc.

Počet nájdených príkladov: 5529

Riešte R
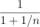Riešte rovnicu so zátvorkami: 5×(2u-9)-8×(0,5-3u)=4×(7u-1)-3
Štvrtina 10
Štvrtina neznámeho čísla zväčšená o sto je päťdesiat. Aké je neznáme číslo?
Oplatka, tyčinka
Jarmila si kúpila oplátku, tyčinku a čokoládu. Zaplatila 38 Kč. Tyčinka bola o 8 Kč drahšia ako oblátka, čokoláda je štyrikrát drahšia ako oblátka. Koľko stála oblátka, tyčinka a čokoláda?
GP - voľná
Pre geometrickú postupnosť platí zaujímavý vzťah medzi prvým a tretím členom: a1-a3=-1,5 a3-a1=1,5 Vypočítajte kvocient q a prvý člen a1.
Ja a otec
Ja a otec máme dnes spolu 55 rokov. Keď budeme mať spolu 65 rokov, bude otec štyrikrát starší ako ja. Koľko mám rokov?
Orechy 8
Peter rozdelil orechy dvom kamarátom. Každý z kamarátov dostal štvrtinu všetkých orechov a ešte dva orechy. Petrovi ostali dva orechy. Koľko orechov mal, keď začal rozdávať?
Traja kamaráti 10
Traja kamaráti Peter, Tomáš a Jirka si zarobili na brigáde 4000Kč. Peter si zarobil trikrát viac ako Tomáš a Jirka o 500 Kč viac ako Tomáš. Koľko zarobil každý z nich?
Do kina 2
V utorok prišlo do kina o 20 návštevníkov viac ako v pondelok. V stredu prišlo dvakrát menej návštevníkov než v utorok. Za tieto tri dni bolo v kine spolu 175 návštevníkov. Koľko ich bolo každý deň?
Čokoláda 10
Anička kúpila tri rovnako čokolády. Tonda kúpil 5 rovnakých čokolád. Tonda zaplatil o 8 eur viac ako Anička. Koľko stala jedna čokoláda?
Záhradkár 5
Záhradkár kúpil 17 jabloní a 11 hrušiek. celkom zaplatil 111,65 eura. Koľko eur stála 1 hruška, ak vieme, že jej cena bola väčšia o 35 centov ako cena 1 jablone? Koľko by záhradkár zaplatil za 28 jabloní a 15 hrušiek?
Anna mala 2
Anna mala 2x viac ako Betka. Cilka mala o 12 eur viac ako Anna. Spolu mali 92 eur. Koľko mala každá?
Červená kytica
Tretina kvietkov v kytici je červená, šesť kvietkov je žltých. Koľko má celkom kytica? A koľko červených?
Dvojnásobok jabĺk
Adam s Bonifácom zbierali jablká. Dohromady nazbierali 77 kg jabĺk. Koľko nazbieral každý z nich keď Adam nazbieral o 5 kg viac, než je dvojnásobok toho, čo nazbieral Bonifác?
Poštové známky
Pavol zbiera poštové známky. Vo svojej zbierke má rovnaký počet korunových a trojkorunových známok, ďalej má päťkorunové známky, ktorých je dvakrát viac ako korunových. Súčet cien uvedených na všetkých známkach je 448 Kč. Koľko známok má Pavol celkom v zb
Neznáme číslo iks
Ak neznáme číslo vynásobím 4 a od výsledku odčítam 8,4, dostanem to isté číslo, ako keď neznáme číslo vynásobím 3 a k výsledku pričítam 15,1. Urči neznáme číslo. Výsledok zapíš v tvare desatinného čísla.
Test MAT
Žiaci písali test z matematiky 5/18 žiakov malo dvojku, 2/9 trojku a 1/6 štvorku. Jednotku malo 12 žiakov. Koľko žiakov písalo test z matematiky?
Prečítať knihu
Jana dostala novú knihu. Chce ju prečítať za 8 dní, keby denne prečítala o 6 strán viac, tak by knihu prečítala o dva dni skôr. Koľko strán má kniha?
Kilometre - beh
Tri kamarátky Jana, Žaneta a Adriana rady behajú. V nedeľu išli všetky behať. Jana ubehla dvakrát viac kilometrov ako Žaneta. Adriana ubehla o 3 kilometre viac ako Žaneta. Koľko kilometrov ubehla Adriana, keď spolu kamarátky ubehli 11 kilometrov?
Malinovky
Koľko zaplatí skautský vedúci za nápoje pre deti, ak si tretina detí dala malinovku za 10 Kc, polovica detí si dala perlivú vodu za 15 Kc a zvyšné 4 deti si dali kofolu za 20 Kc (Kč = české koruny)?
Závisloslé veličiny
Tlačiareň vytlačí k listom za n sekúnd ( k, n ϵ N ). Vyjadrite v závislosti na veličinách k a n počet listov, ktoré tlačiareň vytlačí za 5 minút.

Máš príklad, ktorý si tu nenašiel vyriešenú? Pošli nám tento príklad a my Ti ho skúsime vypočítať.