Angle of two lines
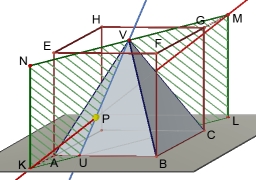
There is a regular quadrangular pyramid ABCDV; | AB | = 4 cm; height v = 6 cm. Determine the angles of lines AD and BV.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
- geometry
- line
- solid geometry
- pyramid
- planimetrics
- right triangle
- triangle
- square
- quadrilateral
- goniometry and trigonometry
- tangent
- arctangent
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Calculate 8354
In a regular pyramid in which the edge of the base is | AB | = 4cm; height = 6cm, calculate the angle of the lines AV and CV, V = vertex. - Distance of points
A regular quadrilateral pyramid ABCDV is given, in which edge AB = a = 4 cm and height v = 8 cm. Let S be the center of the CV. Find the distance of points A and S. - Height of pyramid
The pyramid ABCDV has edge lengths: AB = 4, AV = 7. What is its height? - Wall height
Calculate the surface and volume of a regular quadrangular pyramid if side a = 6 cm and wall height v = 0.8dm.
- Quadrilateral 40551 Find the volume and surface area of a regular quadrilateral pyramid ABCDV if its leading edge has a length a = 10 cm and a body height h = 12 cm.
- Quadrangular pyramid
Given is a regular quadrangular pyramid with a square base. The body height is 30 cm, and volume V = 1000 cm³. Calculate its side and its surface area. - Distance of lines
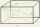Find the distance of lines AE and CG in cuboid ABCDEFGH if given | AB | = 3cm, | AD | = 2 cm, | AE | = 4cm
