Forces
In point, G acts three orthogonal forces: F1 = 16 N, F2 = 7 N, and F3 = 6 N. Determine the resultant of F and the angles between F and forces F1, F2, and F3.
Correct answer:
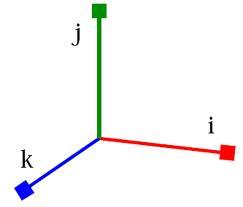
Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
geometryarithmeticsolid geometryplanimetricsnumbersgoniometry and trigonometryUnits of physical quantitiesthemes, topicsGrade of the word problem
Related math problems and questions:
- Two forces 3
Two forces with magnitudes 8 Newtons and 15 Newtons act at a point. Find the angle between the forces if the resultant force is 17 Newtons. - On a mass
The forces F1, and F2 with magnitudes of 40N act on a mass point M. Their resultant has a magnitude of 60N. Determine the angle that the forces F1 and F2 make. - Mass point
Two equal forces of 30 Newtons act on a mass point. Find the magnitude of the resultant force if these forces form an angle of 42°. - Forces
Forces with magnitudes F1 = 42N and F2 = 35N act at a common point and make an angle of 77°12'. How big is their resultant?
- Forces
Determine the resultant of two perpendicular forces F1 = 560 N and the second force 25% smaller. - Three vectors
The three forces whose amplitudes are in ratio 9:10:17 act in the plane at one point to balance. Determine the angles of each of the two forces. - Resultant force
Calculate mathematically and graphically the resultant of three forces with a common center if: F1 = 50 kN α1 = 30° F2 = 40 kN α2 = 45° F3 = 40 kN α3 = 25°
