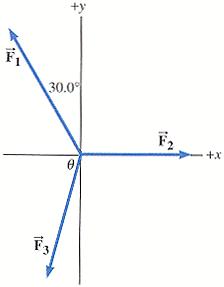
Resultant force
Calculate mathematically and graphically the resultant of three forces with a common center if:
F1 = 50 kN α1 = 30°
F2 = 40 kN α2 = 45°
F3 = 40 kN α3 = 25°
F1 = 50 kN α1 = 30°
F2 = 40 kN α2 = 45°
F3 = 40 kN α3 = 25°
Correct answer:
Tips to related online calculators
Line slope calculator is helpful for basic calculations in analytic geometry. The coordinates of two points in the plane calculate slope, normal and parametric line equation(s), slope, directional angle, direction vector, the length of the segment, intersections of the coordinate axes, etc.
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
Pythagorean theorem is the base for the right triangle calculator.
See also our trigonometric triangle calculator.
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
Pythagorean theorem is the base for the right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Forces
Forces with magnitudes F1 = 42N and F2 = 35N act at a common point and make an angle of 77°12'. How big is their resultant? - Two forces
Two forces with magnitudes of 25 and 30 pounds act on an object at 10° and 100° angles. Find the direction and magnitude of the resultant force. Round to two decimal places in all intermediate steps and your final answer. - Mass point
Two equal forces of 30 Newtons act on a mass point. Find the magnitude of the resultant force if these forces form an angle of 42°. - Bearing
A plane flew 50 km on a bearing 63°20' and the flew on a bearing 153°20' for 140km. Find the distance between the starting point and the ending point. - Two forces
The two forces F1 = 580N and F2 = 630N, have an angle of 59 degrees. Calculate their resultant force, F. - Tetrahedral pyramid
Determine the surface of a regular tetrahedral pyramid when its volume is V = 120 and the angle of the sidewall with the base plane is α = 42° 30'. - Airplane navigation
An airplane leaves an airport and flies to west 120 miles and then 150 miles in the direction S 44.1°W. How far is the plane from the airport (round to the nearest mile)? - Three vectors
The three forces whose amplitudes are in ratio 9:10:17 act in the plane at one point to balance. Determine the angles of each two forces. - The body
The body slides down an inclined plane forming an angle α = π / 4 = 45° under the action of a horizontal plane under the effect of friction forces with acceleration a = 2.4 m/s ^ 2. At what angle β must the plane be inclined so that the body slides on it - Quadrilateral oblique prism
What is the volume of a quadrilateral oblique prism with base edges of length a = 1m, b = 1.1m, c = 1.2m, d = 0.7m, if a side edge of length h = 3.9m has a deviation from the base of 20° 35' and the edges a, b form an angle of 50.5°. - Two forces 3
Two forces of magnitude 8 Newtons and 15 Newtons respectively act at a point. If the resultant force is 17 Newtons, find the angle between the forces. - Side wall planes
Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls. - Forces
In point O acts three orthogonal forces: F1 = 20 N, F2 = 7 N, and F3 = 19 N. Determine the resultant of F and the angles between F and forces F1, F2, and F3. - Hot air balloon
The center of the balloon is at an altitude of 600 m above the ground (AGL). From habitat on earth is the center of the balloon to see in elevation angle 38°20' and the balloon is seen from the perspective of angle 1°16'. Calculate the diameter of the bal - Cosine
Cosine and sine theorem: Calculate all missing values from triangle ABC. c = 2.9 cm; β = 28°; γ = 14° α =? °; a =? cm; b =? cm - A trapezoid
A trapezoid with a base length of a = 36.6 cm, with angles α = 60°, β = 48° and the height of the trapezoid is 20 cm. Calculate the lengths of the other sides of the trapezoid. - Angle of diagonals
Calculate the perimeter and the area of a rectangle if its diagonal is 14 cm and the diagonals form an angle of 130°.
