Sine - practice problems
Number of problems found: 321
- Angle of inclination
Find the angle of inclination of a ramp that rise for 80 cm and is 200 cm long. - Triangle 90
Triangle made by 6 cm 4.5 cm and 7.5 cm. what angles does it make? - A kite 3
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in th - The tent 3
The top of a 1.3 meters tall tent is tethered to the ground by a cable. The cable makes a 37 degrees angle with the ground. Find the cable length. - An electrician 7
An electrician has to repair an electric fault on a pole 4 meters in height. He needs to reach a point 1 m below the top. What should be the length of the ladder that he could use, when inclined at an angle 60° to the horizontal? - X-triangle
Find the length of the x segment in the given triangle drawings. - Trigonometric fx
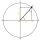When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ.
- Three 235
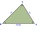Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B. - A right
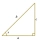A right triangle has side lengths a=3, b=5, and c=4, as shown below. Use these lengths to find tan x, sin x, and cos x. - Subtract polar forms
Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form - Conjugate coordinates
If the rectangular conjugate of the polar vector 12 angle 35 degrees is equal to x+yi, find the sum of x and y. - Cplx sixth power
Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3 - Tunnel - quadrilateral How long will the tunnel AB be, distances AD=35 m, DC=120 m, CB=85 m, and angles ADC=105 degrees and BCD=71 degrees. ABCD is a quadrilateral.
- Parallelogram 44
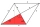Parallelogram ABCD has an area of 32 cm2, lABl=8cm, lBCl=5cm. Calculate the sizes of its interior angles. - Determine the surface area
Find the surface area of a cone of height 30 cm whose side makes an angle of 60° with the base plane.
- Mirror
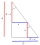The dimensions of the mirror are 750mm x 700mm, the mirror should be tilted 8° from the wall. How many cm must it be tilted from the wall? - Quadrilateral - irregular
Find the length of the side d = |AD| in quadrilateral ABCD: a= 35m, b= 120m, c=85m, angle ABC = 105 degrees, angle BCD= 72 degrees - Unit circle
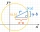In the Cartesian coordinate system, a unit circle is given on which points A and B lie. Point O is the origin and has coordinates (0,0) and point B has coordinates (1,0). The size of angle BOA is 151°. Determine the x-coordinate of point A. - Rhombus 48 A rhombus consists of four identical rhombuses with an area of 42 m². The angle alpha of each rhombus is 60°. What is its perimeter?
- Graduation of the track
The gradient of the track is 9 per mile, and the distance per kilometer (on the slope) [AC] = is 560m. Determine the angle alpha and the distance [AB] = the height between A and B. A / | B/____________C
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
