Sine - practice problems - page 2 of 16
Number of problems found: 320
- Segments on the hypotenuse
A right triangle ABC has a hypotenuse of c=26cm. How many segments does the height vc=12 cm cut out on the hypotenuse c? What are the lengths of the sides a and b? What are the angles at the vertices A and B? - Horizontal 84047
A ladder is leaning against a wall at a height of 6.5 m. How long is the ladder if it makes an angle of 60° with the horizontal floor? - What is 19
What is the length of the hypotenuse c of a right triangle ABC if the angle α at vertex A is 30° and the hypotenuse a = 3cm? - Chord 24
A chord with length t = r times the square root of two divides a circle with radius r into two circular segments. What is the ratio of the areas of these segments?
- Calculate 5
Calculate the area and perimeter of a trapezoid if side a=10, angle alpha 40 degrees, beta 50 degrees, and side c=3. - Staircase - escalator
A moving staircase moves downwards at a speed of 0.6 m/s. The staircase makes an angle of 45° with the horizontal. A person weighing 80 kg walks upwards at a speed of 0.9 m/s. Determine the distance covered by the person and the work done by him before he - Circumscribed circle ABC
Triangle ABC, with sides a = 15 cm, b = 17.4 cm, and c = 21.6 cm, is circumscribed by a circle. Calculate the area of the segments determined by the sides of the triangle. - The chord - angle
The distance of the chord from the center is 6 cm. The central angle is 60°. Calculate the area of the circular segment. - Isosceles 83247
Calculate the lengths of the sides in an isosceles triangle, given the height (to the base) Vc= 8.8cm and the angle at the base alpha= 38°40`.
- Central angle
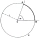A circle k with a center at point S and a radius of 6 cm is given. Calculate the size of the central angle subtended by a chord 10 cm long. - Determine 83081
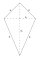A paper kite is shaped like a deltoid ABCD, with two shorter sides 30 cm long, two longer sides 51 cm long, and a shorter diagonal 48 cm long. Determine the sizes of the internal angles of the given deltoid. - Inaccessible 82710
Determine the distance between two inaccessible places K, L, if the angles KAL=62°10", LAB=41°23", KBL=66°34", and LBA were measured from points A, B, which are 870 m apart = 34°52". Thank you. - Observatories A,B
The target C is observed from two artillery observatories, A and B, 296 m apart. At the same time, angle BAC = 52°42" and angle ABC = 44°56". Calculate the distance of the target C from observatory A. - Parallelogram 82695
Given is the parallelogram KLMN, in which we know the side sizes/KL/ = a = 84.5 cm, /KN/ = 47.8 cm, and the angle size at the vertex K 56°40'. Calculate the size of the diagonals.
- Circular segment
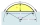A circular segment has an area of 6.04 cm², the central omega angle is 15 degrees, what is the radius? - Cone slope
Determine the volume and surface area of a cone whose slope of length 8 cm makes an angle of 75 degrees with the plane of the base. - Calculate 81950
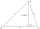The tangent of the angle formed by the adjacent sides of the triangle ABC (side a=29 m, b = 40 m) equals 1.05. Calculate the area of that triangle. - Difference 81888
The ropeway climbs at an angle of 22°30'. Calculate its length if the height difference between the lower and upper station is 560m. Sketch a picture - Perpendicular forces
Distribute the force of magnitude F = 100 N into two perpendicular components with magnitudes F1 and F2 so that the angle between forces F1 and F is 43°52'.
A triangle ABC is located in the plane with a right angle at vertex C, for which the following holds: A(1, 2), B(5, 2), C(x, x+1), where x > -1. a) determine the value of x b) determine the coordinates of point M, which is the midpoint of line segment Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
