Circumscribed circle ABC
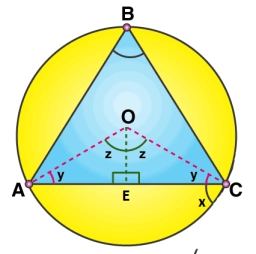
Triangle ABC, with sides a = 15 cm, b = 17.4 cm, and c = 21.6 cm, is circumscribed by a circle. Calculate the area of the segments determined by the sides of the triangle.
Your answer:
Your answer:
Tips for related online calculators
See also our right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetrygoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Triangle - many properties
In a right triangle ABC with a right angle at the vertex C, it is given: a = 17 cm, Vc = 8 cm. Calculate the length of the sides b, c, its area S, the perimeter o, the length of the radii of the circles of the triangle circumscribed by R and inscribed r a - Described circle to rectangle
The rectangle with 6 cm and 4 cm sides was a circumscribed circle. What part of the circle area determined by the circumscribed circle occupies a rectangle? Express in perctentages(%). - Annulus from triangle
Calculate the area of the area bounded by a circle circumscribed and a circle inscribed by a triangle with sides a = 25 mm, b = 29 mm, c = 36 mm. - Circumscribed circle
In triangle ABC, we know a = 4 cm, b = 6 cm, γ = 60°. Calculate the area and radius of the inscribed and circumscribed circle. - Triangle circle radius
Given is an isosceles triangle whose base is 8 cm, and the sides are 15 cm long. Calculate the area of the triangle and the radius of the inscribed and circumscribed circle. - Triangle area and angle
Calculate the area of the triangle ABC, in which you know the side c=5 cm, the angle at the vertex A= 70 degrees, and the ratio of the segments cut by the height to the side c is 1:3 . - Circles 2
Calculate the area of the region between the circumscribed circle and the inscribed circle of a triangle with sides 29 cm, 16 cm, and 21 cm.
