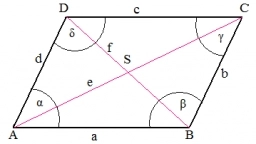
Parallelogram 82695
Given is the parallelogram KLMN, in which we know the side sizes/KL/ = a = 84.5 cm, /KN/ = 47.8 cm, and the angle size at the vertex K 56°40'. Calculate the size of the diagonals.
Correct answer:
Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- arithmetic
- square root
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
- diagonal
- parallelogram
- goniometry and trigonometry
- sine
- cosine
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- KLMN
In the KLMN trapezoid is given this information: 1. segments KL and MN are parallel 2. segments KL and KM have the same length 3. segments KN, NM, and ML have the same length. Determine the size of the angle KMN. - Millimeters 4811
Construct a triangle ABC if you know the lengths of its sides c = 5 cm, a = 4 cm and angle ABC is 60°. Measure the length of side b in millimeters. Side length b is: a, 75 mm < b < 81 mm b, 53 mm < b < 59 mm c, 43 mm < b < 49 mm d, 13 mm - Triangles
Find out whether the given sizes of the angles can be interior angles of a triangle: a) 23°10',84°30',72°20' b) 90°,41°33',48°37' c) 14°51',90°,75°49' d) 58°58',59°59',60°3' - Parallelogram 5027
Calculate the area of the parallelogram if the side sizes are a = 80, b = 60, and the size of the diagonal angle is 60°.
- Right-angled 81150
In the right-angled triangle ABC (the right angle at vertex C), the angle ratio is α : β = 5 : 3. Calculate the sizes of these angles and convert them to degrees and minutes (e.g., 45°20') - Right angle
In a right triangle ABC with a right angle at the apex C, we know the side length AB = 24 cm and the angle at the vertex B = 71°. Calculate the length of the legs of the triangle. - Rhombus diagonals
In the rhombus ABCD are given the sizes of diagonals e = 24 cm; f = 10 cm. Calculate the side length of the diamond and the size of the angles, and calculate the area of the diamond. - Equilateral 2543
a) The perimeter of the equilateral triangle ABC is 63 cm. Calculate the side sizes of the triangle and its height. b) A right isosceles triangle has an area of 40.5 square meters. How big is his circuit? c) Calculate the square's area if the diagonal's s - Rhomboid
The rhomboid sides' dimensions are a= 5cm, b = 6 cm, and the angle's size at vertex A is 60°. What is the length of the side AC?
- Parallelogram
We know about parallelogram ABCD: length |AB| = 76cm, |BC| = 44cm, and angle ∢BAD = 30°. Find the area of the parallelogram. - Calculate 60423
In a right triangle RST with a right angle at the vertex T, we know the lengths of two sides: s = 7.8 cm and t = 13 cm; calculate the third party r. - Resultant force
Calculate mathematically and graphically the resultant of three forces with a common center if: F1 = 50 kN α1 = 30° F2 = 40 kN α2 = 45° F3 = 40 kN α3 = 25° - Hypotenuses 83154
In a right-angled triangle ABC with a right angle at the vertex C, the magnitudes of the hypotenuses are given ta=5, tb=2√10. Calculate the side sizes of triangle ABC and the circle's radius described by this triangle. - Inaccessible 69794
Determine the distance between two inaccessible places P, Q, if the distance between two observation points A, B is 2000m and if you know the size of the angles QAB = 52°40''; PBA = 42°01''; PAB = 86°40'' and QBA = 81°15''. The considered locations A, B,
- Outer angles
The outer angle of the triangle ABC at the A vertex is 71°40 ' outer angle at the vertex B is 136°50'. What size has the inner triangle angle at the vertex C? - Calculate: 6679
In the right triangle ABC, we know the right angle γ, the area S = 48 cm2, and the side a = 8 cm. Calculate: pages b, c - Internal angles
The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det
