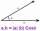
Sum of the two vectors

Vector addition is the operation of adding two (or more) vectors together into a vector sum. The so-called parallelogram law gives the rule for vector addition of two vectors. For two vectors, the vector sum is obtained by placing them head to tail and drawing the vector from the free tail to the free head.

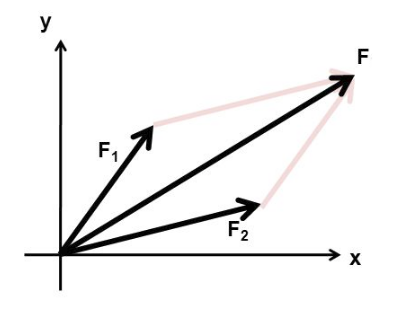
How to add two vectors

If we place the vectors at one starting point, the vectors form two sides of the parallelogram. By completing the remaining two parallel sides, we create a parallelogram. The resulting vector of the sum is the oriented diagonal of this parallelogram starting at the location point of the vectors.

Analytically - by calculation, we calculate the sum of vectors most simply by dividing the vectors into x, y, or z components. We then add the individual vectors by components. We then calculate the size of the resulting vector from the Pythagorean theorem from its component form. We determine the direction vector trigonomically - by the arctangent of the y:x ratio.