Sčítanie vektorov
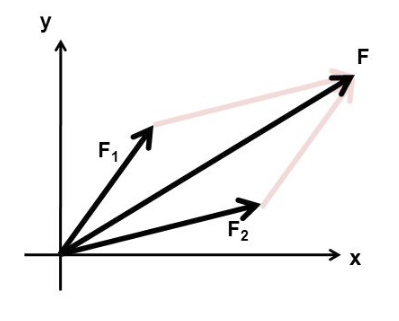
Ako sčítať dva vektory
Graficky možno dva vektory sčítať tak, že na koniec prvého vektora umiesníme začiatok druhého vektora. Výsledný vektor je orientovaná úsečka medzi začiatkom prvého vektora a koncom druhého vektora. Ak vektory umiesníme do jedného začiatočného bodu, vektory sformujú dve strany rovnobežníka. Doplnením zvyšných dvoch rovnobežných strán sformujeme rovnobežník. Výsledný vektor súčtu je orientovanou uhlopriečkou tohto rovnobežníka so začiatkom v bode umiestnenia vektorov.Analyticky - výpočtom vypočítame súčet vektorov najjednoduhšie tak, že vektory rozložíme do zložiek x, y, prípadne z. Jednotlivé vektory potom sčítame po zložkách. Veľkosť výsledného vektora potom dopočítame z Pytagorovej vety z jeho zložkového tvaru. Smerový vektor určíme trigonometricky - arkustangensom pomeru y:x.
Vektory v slovných úlohách
- Vektor
Určite súradnice vektora u=CD, keď C[16;10], D[-10,-18]. - Vektory - základné operácie
Dané sú body A[-13;-18] B[20;9] C[-18; -3] a D[-14;-10] a. Určite súradnice vektorov u=AB v=CD s=DB b. Vypočítajte súčet vektorov u+v c. Vypočítajte rozdiel vektorov u-v d. Určite súradnice vektora w=-2.u - Súradnice vektora
Určte súradnice vektora u = CD, ak C (19; -7) a D (-16; -5) - Vektor umiestnite
Vektor AB, ale A(3,-1), B(5,3) umiestnite do bodu C(1,3) tak že, AB=CO
- Priamka
Priamka p prechádza bodom A[-9, 7] a má smerový vektor v=(-2, -5). Leží bod B[0, 34] na priamke p? - Vzdialenosť rovnobežiek
Zistite vzdialenosť rovnobežiek, ktorej rovnice sú: x=3-4t, y=2+t a x=-4t, y=1+t (návod:na jednej priamke zvoľte bod a zistite jeho vzdialenosť od druhej priamky) - Kolineárne body
Ukážte, že body A (-1,3), B (3,2), C (11,0) sú kolineárne (ležia na jednej priamke). - Vypočítaj 7999 A(5;-4) B(1;3) C(-2;0) D(6;2) Vypočítaj smerový vektor a) a=AB b) b= BC c) c=CD
- Parametrické rovnice
Sú dané body A(1,2), B(4,-2) a C(3,-2) . Nájdite parametrické rovnice priamky, ktorá: a) Prechádza bodom C a je rovnobežná s priamkou AB, b) Prechádza bodom C a je kolmá k priamke AB.
- Lin. závislosť
Zistite či vektory u=(-10; -6) a v=(30; 18) sú lineárne závislé. - Parametrické rovnice
Napíšte parametrické rovnice výšky Vc v trojuholníku ABC: A = [5; 6], B = [- 2; 4], C = [6; -1] - Súradnice ťažiska
Nech A = [3, 2, 0], B = [1, -2, 4] a C = [1, 1, 1] sú 3 body v priestore. Vypočítajte súradnice ťažiska △ ABC (je to priesečník ťažníc). - Vektorová rovnica
Nech v = (1, 2, 1), u = (0, -1, 3) a w = (1, 0, 7) . Vyriešte vektorovú rovnicu c1 v + c2 u + c3 w = 0 pre premenné c1, c2, c3 a rozhodnite, či vektory v, u a w sú lineárne závislé alebo nezávislé - Kolmé 3D vektory
Nájdite vektor a = (2, y, z) tak, aby a⊥b a ⊥ c kde b = (-1, 4, 2) a c = (3, -3, -1)
Nájdite vektor v4 kolmý na vektory v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) a v3 = (0, 0, 1, 1)slovné úlohy - viacej »
