Sčítání vektorů
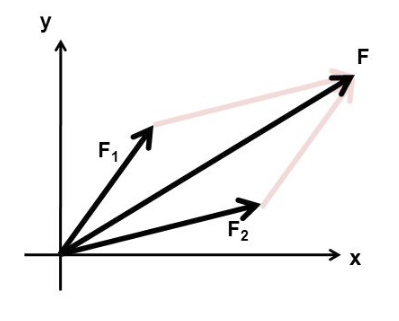
Jak sečíst dva vektory
Pokud vektory umístíme do jednoho počátečního bodu, vektory zformují dvě strany rovnoběžníku. Doplněním zbylých dvou rovnoběžných stran zformujeme rovnoběžník. Výsledný vektor součtu je orientovanou úhlopříčkou tohoto rovnoběžníku se začátkem v bodě umístění vektorů.Analyticky - výpočtem vypočítáme součet vektorů nejjednodušeji tak, že vektory rozložíme do složek x, y, případně z. Jednotlivé vektory pak sečteme po složkách. Velikost výsledného vektoru pak dopočítáme z Pythagorovy věty z jeho složkového tvaru. Směrový vektor určíme trigonometricky - arkustangensem poměru y:x.
Vektory v slovních úlohách
- Vektor
Určitě souřadnice vektoru u=CD, když C[-18;17], D[7,9]. - Vektory - základní operace
Dáno jsou body A [-11; 14] B [-1; -18] C[10; -20] a D[19; 15] a. Určitě souřadnice vektorů u = AB v = CD s = DB b. Vypočítejte vektorový součet u + v c. Vypočítejte rozdíl vektorů u-v d. Určitě souřadnice vektoru w = -4.u - Souřadnice vektoru
Určete souřadnice vektoru u = CD, pokud C (19; -7) a D (-16; -5) - Umístěte vektor
Vektor AB, jestliže A (3, -1), B (5,3) umístěte do bodu C (1,3) tak že, AB = CO
- Přímka
Přímka p prochází bodem A[-3, -2] a má směrový vektor v=(3, -1). Leží bod B[-33, 8] na přímce p? - Rovnoběžek 3314
Zjistěte vzdálenost rovnoběžek, které rovnice jsou: x=3-4t, y=2+t a x=-4t, y=1+t (návod: na jedné přímce zvolte bod a zjistěte jeho vzdálenost od druhé přímky) - Kolineární body
Ukažte, že body A (-1,3), B (3,2), C (11,0) jsou kolineární (leží na jedné přímce). - Směrový vektor A(5;-4) B(1;3) C(-2;0) D(6;2) Vypočítej směrový vektor a) a=AB b) b= BC c) c=CD
- Jsou dány
Jsou dány body A(1,2), B(4,-2) a C(3,-2) . Najděte parametrické rovnice přímky, která: a) Prochází bodem C a je rovnoběžná s přímkou AB, b) Prochází bodem C a je kolmá k přímce AB.
- Lin. závislost
Zjistěte zda vektory u=(-10; 10) a v=(30; -30) jsou lineárně závislé. - Výška parametrická
Napište parametrické rovnice výšky Vc v trojúhelníku ABC: A=[5;6], B=[-2;4], C=[6;-1] - Souřadnice těžiště
Nechť A = [3, 2, 0], B = [1, -2, 4] a C = [1, 1, 1] jsou 3 body v prostoru. Vypočítejte souřadnice těžiště △ ABC (je to průsečík těžnic). - Vektorovou 18193
Nechť v = (1, 2, 1), u = (0, -1, 3) a w = (1, 0, 7) . Vyřešte vektorovou rovnici c1 v + c2 u + c3 w = 0 pro proměnné c1, c2, c3 a rozhodněte, zda vektory v, u a w jsou lineárně závislé nebo nezávislé - Kolmé 3D vektory
Najděte vektor a = (2, y, z) tak, že a⊥b a ⊥ c kde b = (-1, 4, 2) a c = (3, -3, -1)
Najděte vektor v4 kolmý na vektory v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) a v3 = (0, 0, 1, 1)slovní úlohy - více »
