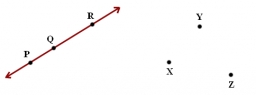
Kolineární body
Ukažte, že body A (-1,3), B (3,2), C (11,0) jsou kolineární (leží na jedné přímce).
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Základem výpočtů v analytické geometrii je dobrá kalkulačka rovnice přímky, která ze souřadnic dvou bodů v rovině vypočítá smernicový, normálový i parametrický tvar přímky, směrnici, směrový úhel, směrový vektor, délku úsečky, průsečíky se souřadnicovým osami atd.
Dva vektory určeny velikostmi a vzájemným úhlem sčítá naše kalkulačka sčítání vektorů .
Dva vektory určeny velikostmi a vzájemným úhlem sčítá naše kalkulačka sčítání vektorů .
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Délka úsečky BC
Body A, B a C jsou kolineární a B leží mezi A a C. Pokud AC = 48, AB = 2x + 2 a BC = 3x + 6, jaká je délka BC? - Přímky
Kolika přímkami lze spojit 8 bodů, pokud tři body leží na jedné přímé a z ostatních žádné tři neleží na téže přímce? - Body v rovině
V rovině je dáno 12 bodů, z nichž 5 leží na jedné přímce. Kolik různých přímek určují dané body? - Kolik 34
Kolik přímek je určeno 5 body, jestliže tři z nich leží v jedné přímce? - Přímka v prostoru
Dané jsou body A [1;a2;a3], B [3;-4;-1], C [-3;-1;8] . Body A, B, C leží na přímce. Vypočítej souradnice a2, a3 - Kružnice
Kolik různých kružnic je určeno 13 body v rovině, jestliže 10 z nich leží v jedné přímce? - Body na přímce
Rozhodněte, zda body A[-2, -5], B[4, 3] a C[16, -1] leží na stejné přímce.
