Směrový vektor
A(5;-4) B(1;3) C(-2;0) D(6;2)
Vypočítej směrový vektor
a) a=AB
b) b= BC
c) c=CD
Vaše odpověď:
Vypočítej směrový vektor
a) a=AB
b) b= BC
c) c=CD
Vaše odpověď:
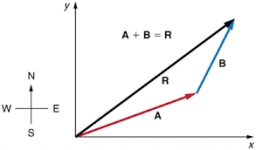
Tipy na související online kalkulačky
Dva vektory určeny velikostmi a vzájemným úhlem sčítá naše kalkulačka sčítání vektorů .
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriearitmetikaplanimetrieÚroveň náročnosti úkolu
Související a podobné příklady:
- Obsah lichoběžníku
Jeden lichoběžník má AB=24M, BC=36M, CD=80M, DA=80M dlouhé strany. Najděte jeho obsah. - Přímka
Přímka p prochází bodem A[-3, -2] a má směrový vektor v=(3, -1). Leží bod B[-33, 8] na přímce p? - Souřadnice vektorů a středů
V rovině je dán trojúhelník ABC. A(-3,5), B(2,3), C(-1,-2) zapište souřadnice vektorů u, v, w pokud u=AB, v=AC, w=BC. Zapište souřadnice středů úseček SAB(. .), SAC(. .. ), SBC(. .. ) - Vektor
Určitě souřadnice vektoru u=CD, když C[-18;17], D[7,9]. - Vektory
Pro vektor w platí: w = +4v. UrčPro vektor w platí: w = +4v. Určete souřadnice vektoru w, jestliže u=(-4, 2), v=(0, 3) - Vektory - základní operace
Dáno jsou body A [-11; 14] B [-1; -18] C[10; -20] a D[19; 15] a. Určete souřadnice vektorů u = AB v = CD s = DB b. Vypočítejte vektorový součet u + v c. Vypočítejte rozdíl vektorů u-v d. Určete souřadnice vektoru w = -4.u - Obvod čtyřúhelníku
Čtyřúhelník ABCD má délky stran AB=13 cm, CD=3 cm, AD=4 cm. Úhly ACB a ADC jsou pravé. Vypočítej obvod čtyřúhelníku ABCD.
