Direction 7999
A (5; -4) B (1; 3) C (-2; 0) D (6; 2)
Calculate the direction vector
a) a = AB
b) b = BC
c) c = CD
Calculate the direction vector
a) a = AB
b) b = BC
c) c = CD
Correct answer:
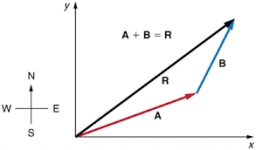
Tips for related online calculators
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
See also our trigonometric triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Four-digit number
For a four-digit number abcd, ab: bc = 1:3 and bc: cd = 2:1 (ab, bc, and cd are two-digit numbers from digits a, b, c, d). Find this number(s). - One trapezium
One trapezium has AB=24M, BC=36M, CD=80M, DA=80M long sides. Find the area. - Trapezoid 70454
Construct a trapezoid ABCD (AB // CD): | AB | = 7cm | BC | = 3.5cm | CD | = 4cm The magnitude of the angle ABC = 60° - Vector - basic operations
There are given points A [-9; -2] B [2; 16] C [16; -2] and D [12; 18] a. Determine the coordinates of the vectors u=AB v=CD s=DB b. Calculate the sum of the vectors u + v c. Calculate the difference of vectors u-v d. Determine the coordinates of the vecto
- Coordinates 32183
The triangle ABC is given in the plane. A (-3,5), B (2,3), C (-1, -2) write the coordinates of the vectors u, v, w if u = AB, v = AC, and w = BC. Enter the coordinates of the centers of the lines SAB (..), SAC (...), SBC (. ..) - Distance of the parallels
Find the distance of the parallels, which equations are: x = 3-4t, y = 2 + t and x = -4t, y = 1 + t (instructions: select a point on one line and find its distance from the other line) - Trapezoid: 18703
In the ABCD trapezoid: | AD | = | CD | = | BC | a | AB | = | AC |. Determine the size of the delta angle.
