Vector perpendicular
Find the vector a = (2, y, z) so that a⊥ b and a ⊥ c where b = (-1, 4, 2) and c = (3, -3, -1)
Correct answer:
Tips for related online calculators
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
geometryalgebraGrade of the word problem
Related math problems and questions:
- Place vector
Place the vector AB if A (3, -1), B (5,3) in point C (1,3) so that AB = CO. - Perpendicular lines
Points A(1,2), B(4,-2) and C(3,-2) are given. Find the parametric equations of the line that: a) It passes through point C and is parallel to the line AB, b) It passes through point C and is perpendicular to line AB. - Parallel and orthogonal
I need math help in this problem: a=(-5, 5 3) b=(-2,-4,-5) (they are vectors) Decompose the vector b into b=v+w where v is parallel to a and w is orthogonal to a, find v and w - Intersection 81611
Given a triangle ABC: A (-1,3), B(2,-2), C(-4,-3). Determine the coordinates of the intersection of the heights and the coordinates of the intersection of the axes of the sides.
- Add vector
Given that P = (5, 8) and Q = (6, 9), find the component form and magnitude of vector PQ. - Right-angled triangle
Determine point C so that triangle ABC is right-angled and isosceles with hypotenuse AB, where A[4,-6], B[-2,10] - A tree 3
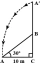A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
