Scalar product - practice problems
Direction: Solve each problem carefully and show your solution in each item.Number of problems found: 26
- Matrices 2
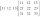Suppose A=(1 6 3 −2) B=(4 −3 −4 3) find 2A+3B - Calculate cuboid
Given cuboid ABCDEFGH. We know that |AB| = 1 cm, |BC| = 2 cm, |AE| = 3 cm. Calculate in degrees the angle size formed by the lines BG and FH . - Determine 82034
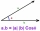The vectors a = (3, -2), b = (-1, 5) are given. Determine the vector c for which a. c = 17; c = 3 - In plane 2
A triangle ABC is located in the plane with a right angle at vertex C, for which the following holds: A(1, 2), B(5, 2), C(x, x+1), where x > -1. a) determine the value of x b) determine the coordinates of point M, which is the midpoint of line segment - Vectors
Find the magnitude of the angle between two vectors u = (3; -5) and v = (10; 6) - Space vectors 3D
The vectors u = (1; 3;- 4) and v = (0; 1; 1) are given. Find their sizes, calculate their angles, and determine the distances between them. - Perpendicular projection
Determine the distance of point B[1, -3] from the perpendicular projection of point A[3, -2] on a straight line 2 x + y + 1 = 0.
- Direction vector The line p is given by the point P [- 0,5; 1] and the direction vector s = (1,5; - 3) determines: A) value of parameter t for points X [- 1,5; 3], Y [1; - 2] lines p B) whether the points R [0,5; - 1], S [1,5; 3] lie on the line p C) parametric equations
- Perpendicular lines
Points A(1,2), B(4,-2) and C(3,-2) are given. Find the parametric equations of the line that: a) It passes through point C and is parallel to the line AB, b) It passes through point C and is perpendicular to line AB. - Vector v4
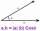Find the vector v4 perpendicular to the vectors v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) and v3 = (0, 0, 1, 1) - Decide 2
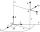Decide whether points A[-2, -5], B[4, 3], and C[16, -1] lie on the same line - Vector perpendicular
Find the vector a = (2, y, z) so that a⊥ b and a ⊥ c where b = (-1, 4, 2) and c = (3, -3, -1) - Vector equation
Let's v = (1, 2, 1), u = (0, -1, 3) and w = (1, 0, 7). Solve the vector equation c1 v + c2 u + c3 w = 0 for variables c1, c2, c3 and decide whether v, u, and w are linear dependent or independent - Angle of the body diagonals
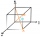Using the vector dot product calculate the angle of the body diagonals of the cube. - Parallel and orthogonal
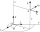I need math help in this problem: a=(-5, 5 3) b=(-2,-4,-5) (they are vectors) Decompose the vector b into b=v+w where v is parallel to a and w is orthogonal to a, find v and w
- Parametric form
Calculate the distance of point A [2,1] from the line p: X = -1 + 3 t Y = 5-4 t Line p has a parametric form of the line equation. - Perpendicular and parallel
Find the value of t if 2tx+5y-6=0 and 5x-4y+8=0 are perpendicular and parallel lines. What angle does each line make with the x-axis, and find the angle between the lines? - Coordinates of square vertices
The ABCD square has the center S [−3, −2] and the vertex A [1, −3]. Find the coordinates of the other vertices of the square. - Scalar product
Calculate the scalar product of two vectors: (2.5) (-1, -4) - Equation of the circle
Find the equation of the circle with the center at (1,20), which touches the line 8x+5y-19=0
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
