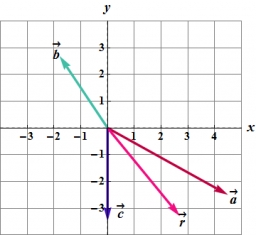
Scalar product
Calculate the scalar product of two vectors: (2.5) (-1, -4)
Final Answer:
Tips for related online calculators
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Scalar dot product
 Calculate u.v if |u| = 5, |v| = 2 and when the angle between the vectors u, v is: a) 60° b) 45° c) 120°
Calculate u.v if |u| = 5, |v| = 2 and when the angle between the vectors u, v is: a) 60° b) 45° c) 120° - In plane 2
 A triangle ABC is located in the plane with a right angle at vertex C, for which the following holds: A(1, 2), B(5, 2), C(x, x+1), where x > -1. a) determine the value of x b) determine the coordinates of point M, which is the midpoint of line segment
A triangle ABC is located in the plane with a right angle at vertex C, for which the following holds: A(1, 2), B(5, 2), C(x, x+1), where x > -1. a) determine the value of x b) determine the coordinates of point M, which is the midpoint of line segment - Scalar products
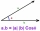 The vectors a = (3, -2), b = (-1, 5) are given. Determine the vector c for which a. c = 17; b . c = 3
The vectors a = (3, -2), b = (-1, 5) are given. Determine the vector c for which a. c = 17; b . c = 3 - Parallel and orthogonal
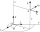 I need math help in this problem: a=(-5, 5 3) b=(-2,-4,-5) (they are vectors) Decompose the vector b into b=v+w where v is parallel to a and w is orthogonal to a, find v and w
I need math help in this problem: a=(-5, 5 3) b=(-2,-4,-5) (they are vectors) Decompose the vector b into b=v+w where v is parallel to a and w is orthogonal to a, find v and w - Vector v4
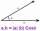 Find the vector v4 perpendicular to the vectors v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) and v3 = (0, 0, 1, 1)
Find the vector v4 perpendicular to the vectors v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) and v3 = (0, 0, 1, 1) - Space vectors 3D
 The vectors u = (1; 3;- 4) and v = (0; 1; 1) are given. Find their sizes, calculate their angles, and determine the distances between them.
The vectors u = (1; 3;- 4) and v = (0; 1; 1) are given. Find their sizes, calculate their angles, and determine the distances between them. - Parametric form
 Calculate the distance of point A [2,1] from the line p: X = -1 + 3 t Y = 5-4 t Line p has a parametric form of the line equation.
Calculate the distance of point A [2,1] from the line p: X = -1 + 3 t Y = 5-4 t Line p has a parametric form of the line equation.
