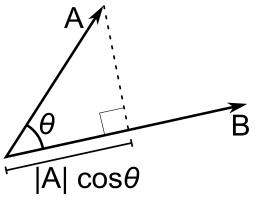
Scalar dot product

Calculate u.v if |u| = 5, |v| = 2 and when the angle between the vectors u, v is:

a) 60°
b) 45°
c) 120°

Correct answer:

a =  5
b =  7.0711
c =  -5

Step-by-step explanation:

u=5 v=2 α=60 ∘  a=u⋅ v⋅ cosα=u⋅ v⋅ cos60° =5⋅ 2⋅ cos60° =5⋅ 2⋅ 0.5=5
β=45 ∘  b=u⋅ v⋅ cosβ=u⋅ v⋅ cos45° =5⋅ 2⋅ cos45° =5⋅ 2⋅ 0.707107=7.071=7.0711
γ=120 ∘  c=u⋅ v⋅ cosγ=u⋅ v⋅ cos120° =5⋅ 2⋅ cos120° =5⋅ 2⋅ (−0.5)=−5

Try another example


Did you find an error or inaccuracy? Feel free to write us. Thank you!







Tips for related online calculators
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.

You need to know the following knowledge to solve this word math problem:

Units of physical quantities:

Grade of the word problem:

Related math problems and questions: