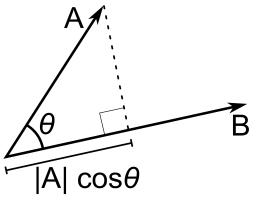
Skalárny súčin
Vypočítajte skalárny súčin vektorov u a v keď |u|=5, |v|=2 a keď vektory u, v, zvierajú uhol:
a) 60°
b) 45°
c) 120°
Vaša odpoveď:
a) 60°
b) 45°
c) 120°
Vaša odpoveď:
Tipy na súvisiace online kalkulačky
Dva vektory určené veľkosťami a vzájomným uhlom sčíta naša kalkulačka sčítania vektorov.
Najprirodzenejšou aplikáciou trigonometrie a goniometrických funkcií predstavuje výpočet trojuholníkov. Bežné aj menej bežné výpočty rôznych typov trojuholníkov ponúka naša trigonometrická kalkulačka trojuholníka. Slovo trigonometria pochádza z gréčtiny a doslovne znamená výpočet trojuholníka.
Najprirodzenejšou aplikáciou trigonometrie a goniometrických funkcií predstavuje výpočet trojuholníkov. Bežné aj menej bežné výpočty rôznych typov trojuholníkov ponúka naša trigonometrická kalkulačka trojuholníka. Slovo trigonometria pochádza z gréčtiny a doslovne znamená výpočet trojuholníka.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
geometriaaritmetikagoniometria a trigonometriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Kolmá a rovnobežné
Potrebujem matematickú pomoc v tomto probléme: sú dané dva trojrozmerné vektory a = (- 5, 5 3) b = (- 2, -4, -5) Rozložte vektor b na b = v + w, kde v je rovnobežná s a a w je kolmá na a. Nájdite súradnice vektorov v a w. - Vektory v priestore 3D
Dané sú vektory u=(1;3;-4), v=(0;1;1). Určte veľkosť týchto vektorov, vypočítajte uhol vektorov, vzdialenosť medzi vektormi. - Skalárny súčin
Vypočítajte skalárny súčin dvoch vektorov: (2,5) (-1, -4) - Vektor v4
Nájdite vektor v4 kolmý na vektory v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) a v3 = (0, 0, 1, 1) - Súčet vektorov
Veľkosť vektora u je 8, vektora v je 4. Vektory zvierajú uhol 59°. Aká je veľkosť vektora u+v? - Skalárne súčiny
Dané sú vektory a = (3, -2), b = (-1, 5). Určte vektor c, pre ktorý platí a. c = 17, b. c = 3 - Vektory - základné operácie
Dané sú body A[-13;-18] B[20;9] C[-18; -3] a D[-14;-10] a. Určte súradnice vektorov u=AB v=CD s=DB b. Vypočítajte súčet vektorov u+v c. Vypočítajte rozdiel vektorov u-v d. Určte súradnice vektora w=-2.u
