Vektory v priestore 3D
Dané sú vektory u=(1;3;-4), v=(0;1;1). Určte veľkosť týchto vektorov, vypočítajte uhol vektorov, vzdialenosť medzi vektormi.
Správna odpoveď:
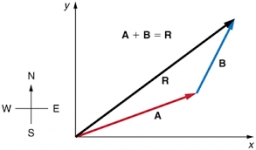
Tipy na súvisiace online kalkulačky
Dva vektory určené veľkosťami a vzájomným uhlom sčíta naša kalkulačka sčítania vektorov.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
geometriaaritmetikaplanimetriagoniometria a trigonometriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Súradnice vektorov
Sú dané vektory v=(2,7; -1,8), w=(-3;2,5). Určte súradnice vektorov: a=v+w, b=v-w, c=w-v, d=2/3v - Vektory - základné operácie
Dané sú body A[-13;-18] B[20;9] C[-18; -3] a D[-14;-10] a. Určte súradnice vektorov u=AB v=CD s=DB b. Vypočítajte súčet vektorov u+v c. Vypočítajte rozdiel vektorov u-v d. Určte súradnice vektora w=-2.u - Kolmá a rovnobežné
Potrebujem matematickú pomoc v tomto probléme: sú dané dva trojrozmerné vektory a = (- 5, 5 3) b = (- 2, -4, -5) Rozložte vektor b na b = v + w, kde v je rovnobežná s a a w je kolmá na a. Nájdite súradnice vektorov v a w. - Medzi vektormi
Určte veľkosť uhla medzi vektormi u =(3; -5) a v = (10;6) - Skalárny súčin
Vypočítajte skalárny súčin vektorov u a v keď |u|=5, |v|=2 a keď vektory u, v, zvierajú uhol: a) 60° b) 45° c) 120° - Sú dané
Sú dané vektory a = (4,2), b = (- 2,1). Vypočítajte: a) |a+b|, b) |a|+|b|, c) |a-b|, d) |a|-|b|. - Vektory - modulus
Urči veľkosť vektorov u= (2,4) a v= (-3,3)
