Space vectors 3D
The vectors u = (1; 3;- 4) and v = (0; 1; 1) are given. Find their sizes, calculate their angles, and determine the distances between them.
Correct answer:
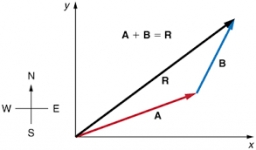
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
See also our right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
See also our right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
- geometry
- line
- vector
- scalar product
- arithmetic
- absolute value
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
- The Law of Cosines
- numbers
- fractions
- goniometry and trigonometry
- cosine
- arccosine
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Cuboids
Two separate cuboids with different orientations are in space. Determine the angle between them, knowing the direction cosine matrix for each separate cuboid. u1=(0.62955056, 0.094432584, 0.77119944) u2=(0.14484653, 0.9208101, 0.36211633) - Calculate 82696
In the triangle ABC, b=5 cm, c=6 cm, /BAC/ = 80° are given. Calculate the sizes of the other sides and angles, and further determine the sizes of the tangent tc and the area of the triangle. - Determine 82034
The vectors a = (3, -2), b = (-1, 5) are given. Determine the vector c for which a. c = 17; c = 3 - Vectors abs sum diff
The vectors a = (4,2), b = (- 2,1) are given. Calculate: a) |a+b|, b) |a|+|b|, c) |a-b|, d) |a|-|b|.
- Coordinates 59763
The vectors v = (2.7; -1.8), w = (-3; 2.5) are given. Find the coordinates of the vectors: a = v + w, b = v-w, c = w-v, d = 2 / 3v - Rhombus diagonals
In the rhombus ABCD, the sizes of the diagonals e = 24 cm and f = 10 cm are given. Calculate the side length of the diamond and the size of the angles, and then calculate the area of the diamond. - Angle between vectors
Find the angle between the given vectors to the nearest tenth degree. u = (6, 22) and v = (10, -11)
