Cuboids
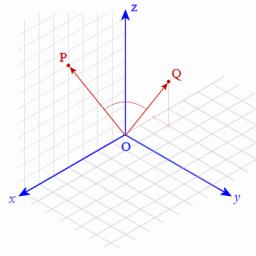
Two separate cuboids with different orientation in space. Determine the angle between them, knowing the direction cosine matrix for each separate cuboid. u1=(0.62955056, 0.094432584, 0.77119944) u2=(0.14484653, 0.9208101, 0.36211633)
Correct answer:
Showing 1 comment:
Matikar
use scalar products to determine angle between two 3D vectors (if direction cosines gives -> its unit vectors)
Tips for related online calculators
Line slope calculator is helpful for basic calculations in analytic geometry. The coordinates of two points in the plane calculate slope, normal and parametric line equation(s), slope, directional angle, direction vector, the length of the segment, intersections of the coordinate axes, etc.
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Cuboid
Cuboid ABCDEFGH with 10 cm height has a base edge length 6 cm and 8 cm. Determine angle between body diagonal and the base plane (round to degrees). - Forces
In point O acts three orthogonal forces: F1 = 20 N, F2 = 7 N, and F3 = 19 N. Determine the resultant of F and the angles between F and forces F1, F2, and F3. - Space diagonal angles
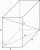Calculate the angle between the body diagonal and the side edge c of the block with dimensions: a = 28cm, b = 45cm and c = 73cm. Then, find the angle between the body diagonal and the plane of the base ABCD. - Space vectors 3D
The vectors u = (1; 3; -4), v = (0; 1; 1) are given. Find the size of these vectors, calculate the angle of the vectors, the distance between the vectors. - Box
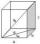Calculate the angle between box base 9 x 14 and body diagonal length 18. - Double-digit 5411
Anička and Blanka each wrote one double-digit number, which started with a seven. The girls chose different numbers. Then each inserted a zero between the two digits, giving them a three-digit number. Everyone subtracted their original two-digit number fr - Diagonal
Determine the dimensions of the cuboid, if diagonal long 60 dm has an angle with one edge 35° and with another edge 77°. - Cuboid - volume, diagonals
The length of the one base edge of cuboid a is 3 cm. Body diagonal is ut=13 cm and diagonal of cuboid's baseis u1=5 cm. What is the volume of the cuboid? - A missile
A missile is fired with a speed of 100 fps in a direction 30° above the horizontal. Determine the maximum height to which it rises? Fps foot per second. - Aircraft
From the aircraft flying at an altitude of 500m, they observed places A and B (at the same altitude) in the direction of flight at depth angles alpha = 48° and beta = 35°. What is the distance between places A and B? - Angle between lines
Calculate the angle between these two lines: p: -8x +4y +5 =0 q: 10x +10y -7=0 - Nice prism
Calculate the cuboid's surface if the sum of its edges is a + b + c = 19 cm and the body diagonal size u = 13 cm. - Measuring 26891
What is the smallest square space we can tile with tiles measuring 25 x 15 cm, knowing there will be no need to cut them? How many tiles will we use? - Faces diagonals
If a cuboid's diagonals are x, y, and z (wall diagonals or three faces), then find the cuboid volume. Solve for x=1.3, y=1, z=1.2 - Components 67664
The force R = 12 N is divided into two components, F1 and F2. Their directions make angles α = 30 °, β = 45 ° with the direction R. What are the components F1, F2? - RWY
Calculate the opposite direction of the runway 13. Runways are named by a number between 01 and 36, which is generally one tenth of the azimuth of the runway's heading in degrees: a runway numbered 09 points east (90°), runway 18 is south (180°), runway 2 - In PE
In PE, students play a game where they do different exercises depending on the color of marble that Coach Forbes draws. Coach Forbes has a jar with 6 red marbles, 12 blue marbles, 16 purple marbles, 2 green marbles, and 4 yellow marbles. What is the proba
