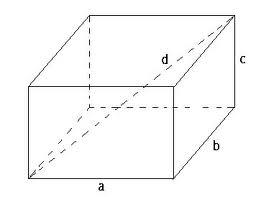
Cuboid
Find the dimensions of cuboids a, b, and c; if diagonal d=6 dm has an angle with edge α=35° and has an angle with edge b β=66°
Final Answer:
Tips for related online calculators
Do you want to convert length units?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
solid geometryplanimetricsnumbersgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Diagonal
Determine the dimensions of the cuboid if it is diagonally long 60 dm and has an angle with one edge 35° and with another edge 77°. - Cuboid - box
The box has the shape of a cuboid with dimensions of 5 cm and 30 mm. Calculate the box's height if the cuboid's volume is 0.60 dm³. Calculate the surface area of the box. (calculation of height from the volume, calculation of area from the formula, keep - Rhomboid
The rhomboid sides' dimensions are a= |AB|=5cm, b = |BC|=6 cm, and the angle's size at vertex A is 60°. What is the length of the diagonal AC? - Quadrilateral prism
Calculate the volume and surface area of a regular quadrilateral prism with base edge a=24 cm if the body diagonal makes an angle of 66° with the base. - Quadrilateral oblique prism
What is the volume of a quadrilateral oblique prism with base edges of length a = 1m, b = 1.1m, c = 1.2m, d = 0.7m if a side edge of length h = 3.9m has a deviation from the base of 20° 35' and the edges a, b form an angle of 50.5°? - Two cuboids
Find the volume of the cuboidal box with one edge: a) 1.4m and b) 2.1 dm. - Space diagonal angles
Calculate the angle between the body diagonal and the side edge c of the block with dimensions: a = 28cm, b = 45cm, and c = 73cm. Then, find the angle between the body diagonal and the plane of the base ABCD.
