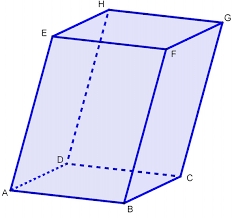
Quadrilateral oblique prism

What is the volume of a quadrilateral oblique prism with base edges of length a = 1m, b = 1.1m, c = 1.2m, d = 0.7m, if a side edge of length h = 3.9m has a deviation from the base of 20° 35 ´ and the edges a, b form an angle of 50.5°.

Correct result:

V =  1.0113 m³

Solution:

$$\begin{gathered} a=1\text{ m } \\ b=1.1\text{ m } \\ c=1.2\text{ m } \\ d=0.7\text{ m } \\ h=3.9\text{ m } \\ \phi =20+35\mathrm{/}60={\displaystyle \frac{247}{12}}\doteq 20.5833^{\circ } \\ \beta =50.5^{\circ } \\ {u}^2=a^2+b^2-2\cdot a\cdot b\cdot \cos \beta \\ u=\sqrt{a^2+b^2-2\cdot a\cdot b\cdot \cos {\beta }^{\circ }}=\sqrt{a^2+b^2-2\cdot a\cdot b\cdot \cos 50.5^{\circ }}=\sqrt{1^2+1.1^2-2\cdot 1\cdot 1.1\cdot \cos 50.5^{\circ }}=\sqrt{1^2+1.1^2-2\cdot 1\cdot 1.1\cdot 0.636078}=0.90035\text{ m } \\ s=(a+b+u)\mathrm{/}2=(1+1.1+0.9003)\mathrm{/}2\doteq 1.5002\text{ m } \\ {S}_1=\sqrt{s\cdot (s-a)\cdot (s-b)\cdot (s-u)}=\sqrt{1.5002\cdot (1.5002-1)\cdot (1.5002-1.1)\cdot (1.5002-0.9003)}\doteq 0.4244\text{ m } \\ {s}_2=(c+d+u)\mathrm{/}2=(1.2+0.7+0.9003)\mathrm{/}2\doteq 1.4002\text{ m } \\ {S}_2=\sqrt{s_2\cdot (s_2-c)\cdot (s_2-d)\cdot (s_2-u)}=\sqrt{1.4002\cdot (1.4002-1.2)\cdot (1.4002-0.7)\cdot (1.4002-0.9003)}\doteq 0.3132\text{ m } \\ {h}_2=h\cdot \sin {\phi }^{\circ }=h\cdot \sin 20.583333333333^{\circ }=3.9\cdot \sin 20.583333333333^{\circ }=3.9\cdot 0.351569=1.37112\text{ m } \\ S=S_1+S_2=0.4244+0.3132\doteq 0.7376\text{ m } \\ V=S\cdot h_2=0.7376\cdot 1.3711=1.0113{\text{m}}^3 \end{gathered}$$

Try calculation via our triangle calculator.

Try another example

Showing 0 comments:

Next similar math problems:

• Quadrilateral prism
  The height of a regular quadrilateral prism is v = 10 cm, the deviation of the body diagonal from the base is 60°. Determine the length of the base edges, the surface, and the volume of the prism.
• Quadrilateral prism
  Calculate the volume (V) and the surface (S) of a regular quadrilateral prism whose height is 28.6 cm and the deviation of the body diagonal from the base plane is 50°.
• Tetrahedral pyramid
  Determine the surface of a regular tetrahedral pyramid when its volume is V = 120 and the angle of the sidewall with the base plane is α = 42° 30´.
• Angle of diagonal
  Angle between the body diagonal of a regular quadrilateral and its base is 60°. The edge of the base has a length of 10cm. Calculate the body volume.
• Diagonal
  Determine the dimensions of the cuboid, if diagonal long 53 dm has an angle with one edge 42° and with another edge 64°.
• Water channel
  The cross section of the water channel is a trapezoid. The width of the bottom is 19.7 m, the water surface width is 28.5 m, the side walls have a slope of 67°30' and 61°15'. Calculate how much water flows through the channel in 5 minutes if the water flo
• Find the area
  Find the area of the triangle with the given measurements. Round the solution to the nearest hundredth if necessary. A = 50°, b = 30 ft, c = 14 ft
• Two chords
  From the point on the circle with a diameter of 8 cm, two identical chords are led, which form an angle of 60°. Calculate the length of these chords.
• Inner angles
  The inner angles of the triangle are 30°, 45° and 105° and its longest side is 10 cm. Calculate the length of the shortest side, write the result in cm up to two decimal places.
• Quadrilateral pyramid
  In a regular quadrilateral pyramid, the height is 6.5 cm and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body. Round calculations to 1 decimal place.
• The pond
  We can see the pond at an angle 65°37'. Its end points are 155 m and 177 m away from the observer. What is the width of the pond?
• Digging a pit
  The pit has the shape of a regular quadrilateral truncated pyramid. The edges of the bases are 14m and 10m long. The sidewalls form an angle of 135° with a smaller base. Determine how many m³ of soil were excavated when digging the pit?
• Viewing angle
  The observer sees a straight fence 60 m long at a viewing angle of 30°. It is 102 m away from one end of the enclosure. How far is the observer from the other end of the enclosure?
• Tetrahedral pyramid
  Calculate the regular tetrahedral pyramid's volume and surface if the content area of the base is 20 cm², and the deviation angle of the side edges from the plane of the base is 60 degrees.
• Four sided prism
  Calculate the volume and surface area of a regular quadrangular prism whose height is 28.6cm and the body diagonal forms a 50-degree angle with the base plane.
• Quadrilateral pyramid
  The regular quadrilateral pyramid has a base edge a = 1.56 dm and a height h = 2.05 dm. Calculate: a) the deviation angle of the sidewall plane from the base plane b) deviation angle of the side edge from the plane of the base
• Two boats
  Two boats are located from a height of 150m above the surface of the lake at depth angles of 57° and 39°. Find the distance of both boats if the sighting device and both ships are in a plane perpendicular to the surface of the lake.