Kosý hranol

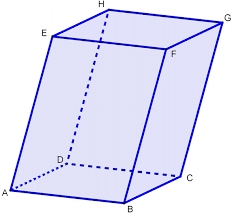
Aký objem má štvorboký kosý hranol s podstavnými hranami o dĺžke a = 1m, b = 1,1m, c = 1,2 m, d = 0,7m, ak bočná hrana s dĺžkou h = 3,9m má odchýlku od podstavy 20° 35 'a hrany a, b zvierajú uhol 50,5°.

Správna odpoveď:

V = 1,0113 m³

Postup správneho riešenia:

a = 1 m b = 1, 1 m c = 1, 2 m d = 0, 7 m h = 3, 9 m φ = 20 + 35 / 60 = \frac{2 4 7}{1 2} ≐ 20, 5833^{\circ} β = 50, 5^{\circ} u^{2} = a^{2} + b^{2} - 2 \cdot a \cdot b \cdot cos β u = a^{2} + b^{2} - 2 \cdot a \cdot b \cdot cos β = a^{2} + b^{2} - 2 \cdot a \cdot b \cdot cos 50, 5 ° = 1^{2} + 1, 1^{2} - 2 \cdot 1 \cdot 1, 1 \cdot cos 50, 5 ° = 1^{2} + 1, 1^{2} - 2 \cdot 1 \cdot 1, 1 \cdot 0, 636078 = 0, 90035 m s = (a + b + u) / 2 = (1 + 1, 1 + 0, 9003) / 2 ≐ 1, 5002 m S_{1} = s \cdot (s - a) \cdot (s - b) \cdot (s - u) = 1, 5002 \cdot (1, 5002 - 1) \cdot (1, 5002 - 1, 1) \cdot (1, 5002 - 0, 9003) ≐ 0, 4244 m s_{2} = (c + d + u) / 2 = (1, 2 + 0, 7 + 0, 9003) / 2 ≐ 1, 4002 m S_{2} = s_{2} \cdot (s_{2} - c) \cdot (s_{2} - d) \cdot (s_{2} - u) = 1, 4002 \cdot (1, 4002 - 1, 2) \cdot (1, 4002 - 0, 7) \cdot (1, 4002 - 0, 9003) ≐ 0, 3132 m h_{2} = h \cdot sin φ = h \cdot sin 20, 583333333333 ° = 3, 9 \cdot sin 20, 583333333333 ° = 3, 9 \cdot 0, 351569 = 1, 37112 m S = S_{1} + S_{2} = 0, 4244 + 0, 3132 ≐ 0, 7376 m V = S \cdot h_{2} = 0, 7376 \cdot 1, 3711 = 1, 0113 m^{3}

Vyskúšajte výpočet cez kalkulačku trojuholníkov.

Našiel si chybu či nepresnosť? Kľudne nám ju napíš.

Tipy na súvisiace online kalkulačky

Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.

Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:

Jednotky fyzikálnych veličín:

objem

Úroveň náročnosti úlohy:

stredná škola

Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1 video2 video3