Kosý hranol
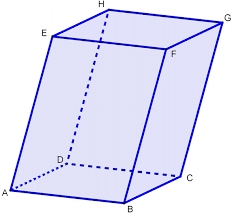
Jaký objem má čtyřboký kosý hranol s podstavnými hranami o délce a=1 m, b=1,1 m, c=1,2 m, d=0,7 m, jestliže boční hrana o délce h=3,9 m má odchylku od podstavy 20°35´ a hrany a, b svírají úhel 50,5°.
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Víte objem a jednotku objemu a chcete proměnit jednotku objemu?
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Víte objem a jednotku objemu a chcete proměnit jednotku objemu?
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraaritmetikastereometrieplanimetriegoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Výška = hrana
V pravidelném čtyřboký jehlanu se výška boční stěny rovná délce hrany podstavy. Obsah boční stěny je 32 cm². Jaký je povrch jehlanu? - Pravidelný 8
Pravidelný čtyřboký jehlan má podstavnou hranu a=1,56 dm a výšku v= 2,05 dm. Vypočtěte : a) odchylku roviny boční stěny od roviny podstavy b) odchylku boční hrany od roviny podstavy - Čtyřboký jehlan 9 Je dán pravidelný čtyřboký jehlan. Délka hrany podstavy a = 6,5 cm, boční hrana s = 7,5 cm. Vypočítejte objem a obsah pláště.
- Pravidelný čtyřboký hranol
Pravidelný čtyřboký hranol má hranu podstavy a=7,1 cm a boční hranu =18,2 cm dlouhou. Vypočítejte jeho objem a povrch. - Květinový záhon
Květinový záhon má tvar komolého jehlanu, přičemž hrana dolní podstavy a = 10 m, horní podstavy b = 9 m a odchylka počne hrany od podstavy je alfa = 45°. Jaký objem zemniny je potřebný navýšit na tento záhon? Kolik sazenic je možné vysadit, pokud 1 m² = 1 - Komolý jehlan 3
Konvice vysoká 35 cm má tvar komolého jehlanu s délkou hrany spodní čtvercové podstavy a=50 cm a s hranami obdélníkové podstavy b=20 cm a c=30 cm. Kolik litru vody se vejde do konvice? - Jehlan
Pravidelný 4-boky jehlan má tělesových výšku 2 dm a protilehlé boční hrany svírají úhel 70°. Vypočtěte povrch a objem jehlanu.
