Příklady na čtyřúhelník
Čtyřúhelník je rovinný geometrický útvar, mnohoúhelník se čtyřmi vrcholy a čtyřmi stranami. Čtyřúhelníky mohou být konvexní (vypouklé) nebo nekonvexní (konkávní, vyduté). Patří sem i rôznobežník, rovnoběžník, obdélník, kosočtverec, čtverec, lichoběžník, deltoid. Součet velikostí vnitřních úhlů čtyřúhelníku je roven 360 ° (2π), což vyplývá z toho, že jej lze úhlopříčkou rozdělit na dva trojúhelníky.Úkol: Každý problém vyřešte pečlivě a předveďte postup řešení každého z nich.
Počet nalezených příkladů: 89
- Obvod čtyřúhelníku
 Čemu se rovná obvod čtyřúhelníku, jehož první strana je o 3 cm delší než druhá strana, třetí strana je o 5 cm kratší než čtvrtá strana a druhá strana je o 2 cm kratší než čtvrtá strana.
Čemu se rovná obvod čtyřúhelníku, jehož první strana je o 3 cm delší než druhá strana, třetí strana je o 5 cm kratší než čtvrtá strana a druhá strana je o 2 cm kratší než čtvrtá strana. - V obecném
 V obecném čtyřúhelníku ABCD je úhel β o 9° větší než úhel α, úhel γ je o 24° větší než úhel α a úhel δ je o 50° větší než úhel β. Urči velikosti jednotlivých úhlů.
V obecném čtyřúhelníku ABCD je úhel β o 9° větší než úhel α, úhel γ je o 24° větší než úhel α a úhel δ je o 50° větší než úhel β. Urči velikosti jednotlivých úhlů. - Úhly čtyřúhelníku
 Ve čtyřúhelníku je úhel α dvakrát větší od úhlu β. úhel γ je 80% úhlu α a úhel δ je o 30° větší od úhlu α. Urč úhly tohoto čtyřúhelníku.
Ve čtyřúhelníku je úhel α dvakrát větší od úhlu β. úhel γ je 80% úhlu α a úhel δ je o 30° větší od úhlu α. Urč úhly tohoto čtyřúhelníku. - Čtvrtá strana
 Obvod čtyřúhelníku (čtyřstranný rovinný útvar) je 125 cm. Pokud tři známé strany měří a = 12 cm, b = 45 cm a c = 30,5 cm, jak dlouhá je čtvrtá strana?
Obvod čtyřúhelníku (čtyřstranný rovinný útvar) je 125 cm. Pokud tři známé strany měří a = 12 cm, b = 45 cm a c = 30,5 cm, jak dlouhá je čtvrtá strana? - Souřadnice bodu Q
 PQRS je čtyřúhelník s P(4,4), S(8,8) a R(12,8). Pokud vektor PQ=4*vektor SR, najděte souřadnice Q. Vyřešte to
PQRS je čtyřúhelník s P(4,4), S(8,8) a R(12,8). Pokud vektor PQ=4*vektor SR, najděte souřadnice Q. Vyřešte to - Výpočty 2
 Výpočty z geometrie: Poměry stran čtyřúhelníku jsou 3 : 6:4,5 : 3,5. Vypočítejte jejich délky, jestliže obvod je 51 cm. Velikosti úhlů v čtyřúhelníku jsou = 29°30´, = 133°10´,= 165°20´. Jaká je velikost úhlu D?
Výpočty z geometrie: Poměry stran čtyřúhelníku jsou 3 : 6:4,5 : 3,5. Vypočítejte jejich délky, jestliže obvod je 51 cm. Velikosti úhlů v čtyřúhelníku jsou = 29°30´, = 133°10´,= 165°20´. Jaká je velikost úhlu D? - Katka MO
 Katka narýsovala trojúhelník ABC. Střed strany AB si označila jako X a střed strany AC jako Y . Na straně BC chce najít takový bod Z, aby obsah čtyřúhelníku AXZY byl co největší. Jakou část trojúhelníku ABC může maximálně zabírat čtyřúhelník AXZY ?
Katka narýsovala trojúhelník ABC. Střed strany AB si označila jako X a střed strany AC jako Y . Na straně BC chce najít takový bod Z, aby obsah čtyřúhelníku AXZY byl co největší. Jakou část trojúhelníku ABC může maximálně zabírat čtyřúhelník AXZY ? - Z8–I–5 MO 2019
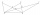 Pro osm navzájem různých bodů jako na obrázku platí, že body C, D, E leží na přímce rovnoběžné s přímkou AB, F je středem úsečky AD, G je středem úsečky AC a H je průsečíkem přímek AC a BE. Obsah trojúhelníku BCG je 12 cm² a obsah čtyřúhelníku DFHG je 8 c
Pro osm navzájem různých bodů jako na obrázku platí, že body C, D, E leží na přímce rovnoběžné s přímkou AB, F je středem úsečky AD, G je středem úsečky AC a H je průsečíkem přímek AC a BE. Obsah trojúhelníku BCG je 12 cm² a obsah čtyřúhelníku DFHG je 8 c - Z6-I-3 2022
 Magda si vystřihla dva stejné rovnoramenné trojúhelníky, z nichž každý měl obvod 100 cm. Nejprve z těchto trojúhelníků složila čtyřúhelník tak, že je k sobě přiložila rameny. Poté z nich složila čtyřúhelník tak, že je k sobě přiložila základnami. V prvním
Magda si vystřihla dva stejné rovnoramenné trojúhelníky, z nichž každý měl obvod 100 cm. Nejprve z těchto trojúhelníků složila čtyřúhelník tak, že je k sobě přiložila rameny. Poté z nich složila čtyřúhelník tak, že je k sobě přiložila základnami. V prvním - Čtyřboký jehlan
 Pravidelný čtyřboký jehlan má objem 24 dm³ a výšku 45 cm. Vypočtěte jeho povrch.
Pravidelný čtyřboký jehlan má objem 24 dm³ a výšku 45 cm. Vypočtěte jeho povrch. - Obsah čtyřúhelníku v čtverci
 Dán je čtverec ABCD. Střed AB je E, střed BC je F, CD je G a střed DA je H. Spojíme AF, BG, CH a DE. Uvnitř čtverce (přibližně uprostřed) průsečíky těchto úseček vytvoří čtyřúhelník. Vypočítejte obsah tohoto čtyřúhelníku. Děkuji
Dán je čtverec ABCD. Střed AB je E, střed BC je F, CD je G a střed DA je H. Spojíme AF, BG, CH a DE. Uvnitř čtverce (přibližně uprostřed) průsečíky těchto úseček vytvoří čtyřúhelník. Vypočítejte obsah tohoto čtyřúhelníku. Děkuji - Výslednice 3
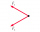 Na hmotný bod působí dvě stejné síly o velikosti 30 N. Urči velikost výslednice, svírají-li tyto síly úhel 42°.
Na hmotný bod působí dvě stejné síly o velikosti 30 N. Urči velikost výslednice, svírají-li tyto síly úhel 42°. - Délka úsečky EF
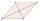 Čtyřúhelník ABCD je souměrný podle úhlopříčky AC. Délka AC je 12 cm, délka BC je 6 cm a vnitřní úhel u vrcholu B je pravý. na stranách AB, AD jsou dány body E, F tak, že trojúhelník ECF je rovnostranný. Určete délku úsečky EF.
Čtyřúhelník ABCD je souměrný podle úhlopříčky AC. Délka AC je 12 cm, délka BC je 6 cm a vnitřní úhel u vrcholu B je pravý. na stranách AB, AD jsou dány body E, F tak, že trojúhelník ECF je rovnostranný. Určete délku úsečky EF. - Úhly deltoidu z draka
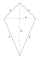 Papírový drak má tvar deltoidu ABCD, ve kterém jsou dvě kratší strany dlouhé po 30 cm, dvě delší strany po 51 cm a kratší úhlopříčka má délku 48 cm. Určete velikosti vnitřních úhlů daného deltoidu.
Papírový drak má tvar deltoidu ABCD, ve kterém jsou dvě kratší strany dlouhé po 30 cm, dvě delší strany po 51 cm a kratší úhlopříčka má délku 48 cm. Určete velikosti vnitřních úhlů daného deltoidu. - Nepravidelný čtyřúhelník
 Vypočítej velikost strany d = |AD| ve čtyřúhelníku ABCD: a= 35m, b= 120m, c=85m, úhel ABC = 105 stupňů, úhel BCD= 72 stupňů
Vypočítej velikost strany d = |AD| ve čtyřúhelníku ABCD: a= 35m, b= 120m, c=85m, úhel ABC = 105 stupňů, úhel BCD= 72 stupňů - Z6-I-6 MO 2018
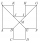 Ve dvanáctiúhelníku ABCDEF GHIJKL jsou každé dvě sousední strany kolmé a všechny strany s výjimkou stran AL a GF jsou navzájem shodné. Strany AL a GF jsou oproti ostatním stranám dvojnásobně dlouhé. Úsečky BG a EL se protínají v bodě M a rozdělují dvanáct
Ve dvanáctiúhelníku ABCDEF GHIJKL jsou každé dvě sousední strany kolmé a všechny strany s výjimkou stran AL a GF jsou navzájem shodné. Strany AL a GF jsou oproti ostatním stranám dvojnásobně dlouhé. Úsečky BG a EL se protínají v bodě M a rozdělují dvanáct - Tunel - čtyřúhelník
 Jak dlouhý bude tunel AB, vzdálenosti AD=35 m, DC=120 m, CB=85 m a úhly ADC=105 stupňů a BCD=71 stupňů. ABCD je čtyřúhelník.
Jak dlouhý bude tunel AB, vzdálenosti AD=35 m, DC=120 m, CB=85 m a úhly ADC=105 stupňů a BCD=71 stupňů. ABCD je čtyřúhelník. - Čtyřúhelník
 Čtyřúhelník ABCD je složen ze dvou pravoúhlých trojúhelníků ABD a BCD. Pro délky stran platí: | AD | = 3cm, | BC | = 12cm, | BD | = 5cm. Kolik centimetrů čtverečních má čtyřúhelník ABCD? Úhly DAB a DBC jsou pravé.
Čtyřúhelník ABCD je složen ze dvou pravoúhlých trojúhelníků ABD a BCD. Pro délky stran platí: | AD | = 3cm, | BC | = 12cm, | BD | = 5cm. Kolik centimetrů čtverečních má čtyřúhelník ABCD? Úhly DAB a DBC jsou pravé. - Obvod zahrady
 Čtyři strany zeleninové zahrady jsou 15 1/2 stopy, 18 3/4 stopy, 24 1/4 stopy a 30 1/2 stopy (1 stopa = 1 ft = 0,30 m). Kolik stop oplocení je zapotřebí k obejití zahrady? (odpověď napište jako celé číslo)
Čtyři strany zeleninové zahrady jsou 15 1/2 stopy, 18 3/4 stopy, 24 1/4 stopy a 30 1/2 stopy (1 stopa = 1 ft = 0,30 m). Kolik stop oplocení je zapotřebí k obejití zahrady? (odpověď napište jako celé číslo) - Čtvrtá strana čtyřúhelníku
 Obvod čtyřúhelníku je 442,95 cm. Tři známé strany měří 84,56 cm, 132,77 cm a 82,75 cm. Jak dlouhá je čtvrtá strana?
Obvod čtyřúhelníku je 442,95 cm. Tři známé strany měří 84,56 cm, 132,77 cm a 82,75 cm. Jak dlouhá je čtvrtá strana?
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
