Katka MO
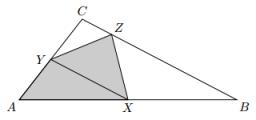
Katka narýsovala trojúhelník ABC. Střed strany AB si označila jako X a střed strany AC jako Y . Na straně BC chce najít takový bod Z, aby obsah čtyřúhelníku AXZY byl co největší. Jakou část trojúhelníku ABC může maximálně zabírat čtyřúhelník AXZY ?
Správná odpověď:
Zobrazuji 1 komentář:
Petr
Nápověda. Určete, jakou část trojúhelníku ABC zabírá trojúhelník AXY.
Ze zadání plyne, že úsečka XY je střední příčkou trojúhelníku ABC, která je rovnoběžná se stranou BC. Její délka je tedy poloviční vzhledem k délce strany BC a velikost výšky z bodu A na XY je taktéž poloviční vzhledem k velikosti výšky z téhož bodu na BC. To znamená, že trojúhelník AXY má čtvrtinový obsah vzhledem k obsahu trojúhelníku ABC.
Nyní zvolme bod Z na straně BC. Protože úsečky BC a XY jsou rovnoběžné, je obsah trojúhelníku XY Z, tedy i čtyřúhelníku XZY stejný pro jakkoli zvolený bod Z. Protože vzdálenost rovnoběžek BC a XY je stejná jako vzdálenost XY od vrcholu A, mají trojúhelníky AXY a XY Z tutéž velikost výšky na jejich společnou stranu XY , a proto mají tentýž obsah. Každý z těchto dvou trojúhelníků zabírá čtvrtinu trojúhelníku ABC, čtyřúhelník AXZY proto zabírá polovinu trojúhelníku ABC.
autor: A. Bohiniková
Ze zadání plyne, že úsečka XY je střední příčkou trojúhelníku ABC, která je rovnoběžná se stranou BC. Její délka je tedy poloviční vzhledem k délce strany BC a velikost výšky z bodu A na XY je taktéž poloviční vzhledem k velikosti výšky z téhož bodu na BC. To znamená, že trojúhelník AXY má čtvrtinový obsah vzhledem k obsahu trojúhelníku ABC.
Nyní zvolme bod Z na straně BC. Protože úsečky BC a XY jsou rovnoběžné, je obsah trojúhelníku XY Z, tedy i čtyřúhelníku XZY stejný pro jakkoli zvolený bod Z. Protože vzdálenost rovnoběžek BC a XY je stejná jako vzdálenost XY od vrcholu A, mají trojúhelníky AXY a XY Z tutéž velikost výšky na jejich společnou stranu XY , a proto mají tentýž obsah. Každý z těchto dvou trojúhelníků zabírá čtvrtinu trojúhelníku ABC, čtyřúhelník AXZY proto zabírá polovinu trojúhelníku ABC.
autor: A. Bohiniková
6 let 1 Like
Tipy na související online kalkulačky
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Téma:
Úroveň náročnosti úkolu:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Trojúhelník
V trojúhelníku ABC se stranou BC délky 2 cm je bod K středem strany AB. Body L a M rozdělují stranu AC na tři shodné úsečky. Trojúhelník KLM je rovnoramenný s pravým úhlem u vrcholu K. Určete délky stran AB, AC trojúhelníku ABC. - Trojúhelník KLB
Je dán rovnostranný trojúhelník ABC. Z bodu L který je středem strany BC tohoto trojúhelníku, je spuštěna kolmice k na stranu AB. Průsečík kolmice k a strany AB je označen jako bod K. Kolik % z obsahu trojúhelníku ABC tvoří trojúhelník KLB? - Podobný
Pokud trojúhelník ABC ~ (podobný) trojúhelníku XYZ, AC = 24, AB = 15, BC = 17 a XY = 9, jaký je obvod trojúhelníku XYZ? Zaokrouhlete všechny strany na 1 desetinné místo. - Střední příčka
Trojúhelník ABC je rovnostranný o straně délky 8 cm. Body D, E, F jsou postupně středy stran AB, BC, AC. Vypočtěte obsah trojúhelníku DEF. V jakém poměru je obsah trojúhelníku ABC k obsahu trojúhelníku DEF? - Zaokrouhlenou 38351
Ivan a Katka objevili na dovolené pravidelný jehlan, jehož podstavou byl čtverec se stranou 230 ma jehož výška byla rovna poloměru kruhu se stejným obsahem jako podstavný čtverec. Katka označila vrcholy čtverce ABCD. Ivan vyznačil na přímce spojující bod - Trojúhelníku 47071
V trojúhelníku ABC, pravoúhlý úhel je na vrcholu B. Strany /AB/=7cm, /BC/=5cm, /AC/=8,6cm. Najděte na dvě desetinná místa. A. sinus úhlu C B. Kosinus C C. Tangenta C. - Kružnice 14683
Bod B je střed kružnice. Přímka AC se dotýká kružnic v bodě C a platí AB=20 cm a AC=16 cm. Jaký je poloměr kružnice BC? - MO Z7–I–6 2021
V trojúhelníku ABC leží na straně AC bod D a na straně BC bod E. Velikosti úhlů ABD, BAE, CAE a CBD jsou postupně 30°, 60°, 20° a 30°. určete velikost úhlu AED. - Trojúhelníku 4908
Lichoběžník ABCD se základnami AB=a, CD=c má výšku v. Bod S je střed ramene BC. Dokažte, že obsah trojúhelníku ASD se rovná polovině obsahu lichoběžníku ABCD. - Z9 – I – 2 MO 2018
V rovnostranném trojúhelníku ABC je K středem strany AB, bod L leží v třetině strany BC blíže bodu C a bod M leží v třetině strany AC blíže bodu A. Určete, jakou část obsahu trojúhelníku ABC zabírá trojúhelník KLM. - Sestrojený čtverce
Na dvěma stranami trojúhelníku ABC jsou sestrojeny čtverce. Obsah čtverce nad stranou BC je 25 cm². Velikost výšky vc na stranu AB je 3 cm. Pata P výšky vc dělí stranu AB v poměru 2 : 1. Strana AC je delší než strana BC. Vypočtěte v cm délku strany AB. Vy - Z8–I–5 MO 2019
Pro osm navzájem různých bodů jako na obrázku platí, že body C, D, E leží na přímce rovnoběžné s přímkou AB, F je středem úsečky AD, G je středem úsečky AC a H je průsečíkem přímek AC a BE. Obsah trojúhelníku BCG je 12 cm² a obsah čtyřúhelníku DFHG je 8 c - Rovnoramenný 2588
Daný je rovnoramenný lichoběžník ABCD, ve kterém platí |AB|= 2|BC|= 2|CD|= 2|DA|. Na jeho straně BC je bod K takový, že |BK| = 2|KC|, na jeho straně CD je bod L takový, že |CL|= 2|LD|, a na jeho straně DA je bod M takový, že|DM|= 2|MA|. Určete velikosti v - V čtverci
V čtverci ABCD se stranou a = 6 cm je bod E střed strany AB a bod F střed strany BC. Vypočítejte velikost všech úhlů trojúhelníku DEF a délky jeho stran. - Čtverec JKLM
Čtverec JKLM má strany délky 24 cm. Bod S je středem LM. Vypočítejte obsah čtyřúhelníku JKSM v cm². - Úhel x
Úhel x je oproti straně AB, která je dlouhá 10 a strana AC je dlouhá 15 a je přeponou v trojúhelníku ABC. Vypočtěte úhel x. - Čtyřúhelník
Ve čtverci ABCD je bod P uprostřed strany DC a bod Q uprostřed strany AD. Pokud obsah čtyřúhelníku BQPC je 49 cm2, jaký je obsah ABCD?
