Matematická olympiáda - příklady
Úkoly MO nejsou lehké, ani pro dospělé lidi. Zároveň věříme, že správné řešení, které je zde publikované téměř na jeden klik poslouží jen na inspiraci. V reálném životě každý totiž řeší úkoly, které nikdo jiný před tím neřešil.Nenechte se odradit, když neobjevíte hned řešení. Experimentujte, kreslete si, "hrajte se" s úlohou. Někdy pomůže podívat se do nějaké knížky, kde najdete podobné úkoly vyřešeny, jindy se může stát, že najednou o tři dny "z ničeho nic" na řešení přijdete.
Počet nalezených příkladů: 207
- MO Z7 2025
Andulka a Zuzana pojídaly švestky. První den snědla Andulka tři čtvrtiny toho, co týž den snědla Zuzana. Druhý den snědla Zuzana tři poloviny toho, co týž den snědla Andulka. Dohromady za oba dny snědly 31 švestek a každé děvče každý den snědlo celý počet - Jednociferné číslo
Rozhodněte, zda lze k číslu s ciferným součtem 2024 připočítat jednociferné číslo tak, aby výsledné číslo mělo ciferný součet 74. - Polokružnice 84046
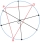V obdélníku se stranami délek 4cm a 8cm leží dvě různé polokružnice, z nichž každá má krajní body v jeho sousedních vrcholech a dotýká se protilehlé strany. Sestrojte čtverec takový, že jeho dva vrcholy leží na jedné polokružnici, zbylé dva na druhé a jeh - Z6–I–5 MO 2024
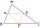Péťa složil z navzájem shodných trojúhelníků několik rovinných útvarů. Obvody prvních tří jsou postupně 8 cm, 11,4 cm a 14,7 cm. Určete obvod čtvrtého útvaru
- Představují 82998
Adam napsal následující součet s pěti tajnými sčítanci: a + bb + ccc + dddd + eeeee. Prozradil, že znaky „a, b, c, d, e“ představují navzájem různé číslice 1, 2, 3, 4, 5 a že výsledný součet je dělitelný 11. Které nejmenší a které největší číslo může být - Pravoúhlý 37
Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce. - MO z5 2024
Anetčin strýc má narozeniny ve stejný den v roce jako Anetčina teta. Strýc je starší než teta, ne však o víc než o deset let, a oba jsou plnoletí. Na poslední oslavě jejich narozenin si Anetka uvědomila, že když vynásobí jejich oslavované věky a výsledný - Čtyřúhulník AFHD
Trojúhelník ABC je rozdělen úsečkami. Úsečky DE a AB jsou rovnoběžné. Trojúhelníky CDH, CHI, CIE, FIH mají stejný obsah a to 8 dm². Zjistěte obsah čtyřúhelníku AFHD. - Pravidelně 82605
Zajíc se zúčastnil závodu dlouhých 2024 metrů. Ze startovní čáry se odrazil levou nohou a po celou dobu závodu pravidelně střídal levou, pravou a obě nohy. Když se zajíc odrazil levou nohou, skočil 35 dm, když se odrazil pravou nohou, skočil 15 dm, a když
- Nepozornosti MO 2023 Z9 Karel měl vynásobit dvě dvouciferná čísla. Z nepozornosti vyměnil pořadí číslic v jednom z činitelů a dostal součin, který byl o 4 248 menší než správný výsledek. Jaký je správný výsledek? Kolik mělo Karlovi správně vyjít?
- Zahrádkařské 82494
V zahrádkařské osadě měl pan Jahoda ve svém sudu 16.litrů vody. Soused Malina měl ve svém sudu třikrát více vody, než pan Jahoda. Začalo pršet a do obou sudů napršelo stejné množství vody. Po dešti pan Malina zjistil, že má v sudu dvakrát více vody, než p - Rozhodněte 82454
Adam měl papír, který byl natolik velký, že by se z něj dalo natrhat několik desítek tisíc kousků. Nejprve papír roztrhal na čtyři kousky. Každý z těchto kousků vzal a roztrhal buď na čtyři, nebo na deset kousků. Stejným způsobem pokračoval dál: každý nov - V loňském
V loňském roce bylo v našem skautském oddíle o 30 chlapců více než děvčat. Letos se počet dětí v oddíle zvětšil o 10% přičemž počet chlapců se zvětšil o 5% a počet děvčat se zvětšil o 20%. Kolik dětí máme letos v oddíle? - Myslím 20 Myslím si tři čísla, když je sečtou dostanu 16, když od součtu prvních dvou čísel odečtou třetí dostanu 10, když od součtu prvního a třetího čísla odečtou druhé dostanu 8. Která čísla si myslím?
- Čtyřúhelníku 81469
Dán je čtverec ABCD. Střed AB je E, střed BC je F, CD je G a střed DA je H. Spojíme AF, BG, CH a DE. Uvnitř čtverce (přibližně uprostřed) průsečíky těchto úseček vytvoří čtyřúhelník. Vypočítejte obsah tohoto čtyřúhelníku. Děkuji - Z6-I-3 2022
Magda si vystřihla dva stejné rovnoramenné trojúhelníky, z nichž každý měl obvod 100 cm. Nejprve z těchto trojúhelníků složila čtyřúhelník tak, že je k sobě přiložila rameny. Poté z nich složila čtyřúhelník tak, že je k sobě přiložila základnami. V prvním - Z7–I–5 MO 2022
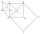Na obrázku jsou znázorněny čtverce ABCD, EFCA, CHCE a IJHE. Body S, B, F a G jsou po řadě středy těchto čtverců. Úsečka AC je dlouhá 1 cm. Určete obsah trojúhelníku IJS. Prosím pomozte... - MO z7 2022
Jsou také dva rovnostranné trojúhelníky ABC a BDE tak že velikost úhlu ABD je větší než 120° a menší než 180° bod C, E leží ve stejné polorovině vymezené přímkou AD. Průsečík CD a AE je označen F. Určete velikost úhlu AFD. - Mo z9 2022 čtverce
Vrcholy čtverce ABCD spojuje lomená čára DEFGHB. Menší úhly u vrcholů E, F, G, H jsou pravé a úsečky DE, EF, FG, GH, HB po řadě měří 6 cm, 4cm, 4 cm, 1 cm, 2 cm. Určete obsah čtverce ABCD.
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
