Mathematical Olympiad - practice problems
MO tasks are not easy, even for adults. At the same time, we believe that the right solution, which is here published almost on one click will serve as the inspiration.Do not be discouraged if you did not discover the right solution. Experiment, sketching, "play" with the problem. Sometimes it helps to look into a book and find out similar problems resolved. Sometimes help three days pause, and then you found the right solution.
Number of problems found: 210
- MO Z7 2025
Adela and Susan ate plums. On the first day, Adela ate three quarters of what Susan ate that day. On the second day, Susan ate three halves of what Adela ate that day. Together, they ate 31 plums over the two days, and each girl ate a whole number of plum - Digit sum MO Z9-I-4
Determine whether it is possible to add a single-digit number to a number with a digit sum of 2,024 so that the resulting number has a digit sum of 74. - Semicircles
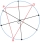In a rectangle with sides of 4 cm and 8 cm, there are two different semicircles, each with its endpoints at adjacent vertices and touching the opposite side. Construct a square such that two of its vertices lie on one semicircle, the other two vertices li - Shape perimeter fourth
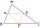Péta composed several planar shapes from mutually congruent triangles. The circumferences of the first three are 8 cm, 11.4 cm, and 14.7 cm, respectively. Determine the perimeter of the fourth shape. - Number sum divisibility
Adam wrote the following sum with five secret adders: a + bb + ccc + dddd + eeeee. He revealed that the characters "a, b, c, d, e" represent the different digits 1, 2, 3, 4, and 5 and that the resulting sum is divisible by 11. Which is the smallest and wh - Triangle square area
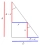A right triangle has an area of 36 cm². A square is placed in it so that two sides of the square are parts of two sides of a triangle, and one vertex of the square is in a third of the longest side. Determine the area of this square. - Mo z5 2023 dogs
Anetka's uncle has his birthday on the same day of the year as Anetka's aunt. The uncle is older than the aunt, but not by more than ten years, and both are of full legal age. At the last celebration of their birthdays, Anetka realised that when she multi - Line segments
Triangle ABC is divided by line segments. Lines DE and AB are parallel. Two lines are drawn from vertex C. The first line intersects points H and F on segments DE and AB. The second line intersects points I and G on segments DE and AB. Triangles CDH, CHI, - Hare 2024m
A hare participated in a race 2024 metres long. From the starting line he pushed off with his left foot and throughout the race he regularly alternated left, right, and both feet. When the hare pushed off with his left foot, he jumped 35 dm, when he pushe - Karel digit error Carl had to multiply two two-digit numbers. Out of care, he changed the order of the digits in one of the factors and got a product that was 4,248 less than the correct result. What is the correct result? How much should Karl have earned?
- Gardening
In the allotment garden, Mr. Strawberry had 16 litres of water in his barrel. His neighbour Mr. Malina had three times more water in his barrel than Mr. Strawberry. It then started to rain, and the same amount of rainwater fell into both barrels. After th - Adam had 3
Adam had paper which was so large that several tens of thousands of pieces could be torn from it. First he tore the paper into four pieces. Each of these pieces he took and tore either into four or into ten pieces. In the same way he continued further: ea - Scout troop increase
Last year, there were 30 more boys than girls in our scout troop. This year, the number of children in the ward increased by 10%, while the number of boys increased by 5% and the number of girls increased by 20%. How many children do we have in the depart - Number sum subtraction I think of three numbers; when I add them, I get 16; when I subtract the third from the sum of the first two numbers, I get 10; when I subtract the second from the sum of the first and third numbers, I get 8. Which numbers do I think?
- Quadrilateral calc
The square ABCD is given. The midpoint of AB is E, the midpoint of BC is F, CD is G, and the midpoint of DA is H. Join AF, BG, CH, and DE. Inside the square (approximately in the middle), the intersections of these line segments form a quadrilateral. Calc - MO Z6-I-3 2022
Magda cut out two identical isosceles triangles, each of which had a perimeter of 100 cm. First, from these triangles she formed a quadrilateral by placing them together by their legs. Then from them she formed a quadrilateral by placing them together by - Square triangle area
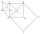The figure shows the squares ABCD, EFCA, CHCE, and IJHE. Points S, B, F, and G are, respectively, the centers of these squares. Line segment AC is 1 cm long. Determine the area of triangle IJS. Please help... - Triangle angle operations
There are also two equilateral triangles ABC, and BDE, such that the size of the angle ABD is greater than 120° and less than 180° points C and E lie in the same half-plane defined by the line AD. The intersection of CD and AE is marked F. Determine the s - Square broken line
The vertices of the square ABCD are joined by the broken line DEFGHB. The smaller angles at the vertices E, F, G, and H are right angles, and the line segments DE, EF, FG, GH, and HB measure 6 cm, 4 cm, 4 cm, 1 cm, and 2 cm, respectively. Determine the ar - Eva number product Eve thought of two natural numbers. She first added these correctly, then subtracted them correctly. In both cases, she got a double-digit result. The product of the resulting two-digit numbers was 645. Which numbers did Eve think of? Please, what is this
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
