Determine 82724
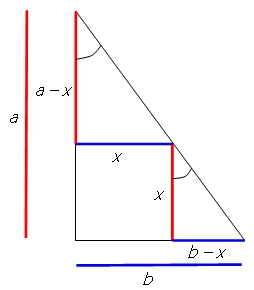
A right triangle has an area of 36 cm2. A square is placed in it so that two sides of the square are parts of two sides of a triangle, and one vertex of the square is in a third of the longest side.
Determine the area of this square.
Determine the area of this square.
Correct answer:
Showing 1 comment:
Math student
Given: (ab)/2 = 36; ab = 72
Let: c = sqrt(aˆ2 + bˆ2)
(b-x)/(c/3) = x/((2c)/3)); b = (3x)/2
(a-x)/((2c)/3)) = a/c; a = 3x
ab = (3x)((3x)/2) = 72
Therefore, xˆ2 = 16.
Let: c = sqrt(aˆ2 + bˆ2)
(b-x)/(c/3) = x/((2c)/3)); b = (3x)/2
(a-x)/((2c)/3)) = a/c; a = 3x
ab = (3x)((3x)/2) = 72
Therefore, xˆ2 = 16.
Tips for related online calculators
See also our right triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- An equilateral
An equilateral triangle is inscribed in a square of side 1 unit long so that it has one common vertex with the square. What is the area of the inscribed triangle? - Recursion squares
In the square, ABCD has inscribed a square so that its vertices lie at the centers of the sides of the square ABCD. The procedure of inscribing the square is repeated this way. The side length of the square ABCD is a = 20 cm. Calculate: a) the sum of peri - Quadrilateral 81097
The quadrilateral ABCD is symmetrical about the diagonal AC. The length of AC is 12 cm, the length of BC is 6 cm, and the interior angle at vertex B is right. points E and F are given on the sides AB, and AD so that the triangle ECF is equilateral. Determ - Integer sides
A right triangle with an integer length of two sides has one leg √11 long. How long is its longest side?
- Two-fifths 5337
The triangle is divided into three parts. The part at the vertex C occupies a third of the area of the triangle, the part at the vertex B is two-fifths of the area of the triangle, and the remaining part at the vertex A has an area of 4 m². Calculate the - Rafael
Rafael has three squares. The first square has a side length of 2 cm. The second square has a side length of 4 cm, and its vertex is placed in the center of the first square. The last square has a side length of 6 cm, and its vertex is placed in the cente - Intersection 81611
Given a triangle ABC: A (-1,3), B(2,-2), C(-4,-3). Determine the coordinates of the intersection of the heights and the coordinates of the intersection of the axes of the sides.
