Mathematical Olympiad - practice problems - page 8 of 9
Number of problems found: 178
- Z9–I–1
 All nine fields of given shape are to be filled with natural numbers so that: • each of the numbers 2, 4, 6, and 8 is used at least once, • four of the inner square boxes containing the products of the numbers of adjacent cells of the outer square, • in t
All nine fields of given shape are to be filled with natural numbers so that: • each of the numbers 2, 4, 6, and 8 is used at least once, • four of the inner square boxes containing the products of the numbers of adjacent cells of the outer square, • in t - Mrak - cloud
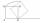 It is given segment AB, which is 12 cm in length, on which one side of the square MRAK is laid. MRAK's side length is 2 cm shown. MRAK gradually flips along the line segment AB, and point R leaves a paper trail. Draw the whole track of point R until the s
It is given segment AB, which is 12 cm in length, on which one side of the square MRAK is laid. MRAK's side length is 2 cm shown. MRAK gradually flips along the line segment AB, and point R leaves a paper trail. Draw the whole track of point R until the s - Educational trails
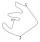 From point A to point C, an educational trail passes through point B and a red tourist sign; see the picture. In addition, an undrawn abbreviation 1500 meters long, starting at A and ending on the nature trail, can be used. Vojtech found that • the trip f
From point A to point C, an educational trail passes through point B and a red tourist sign; see the picture. In addition, an undrawn abbreviation 1500 meters long, starting at A and ending on the nature trail, can be used. Vojtech found that • the trip f - MO SK/CZ Z9–I–3
 John had the ball that rolled into the pool and swam in the water. Its highest point was 2 cm above the surface. The circle's diameter that marked the water level on the ball's surface was 8 cm. Find the diameter of John's ball.
John had the ball that rolled into the pool and swam in the water. Its highest point was 2 cm above the surface. The circle's diameter that marked the water level on the ball's surface was 8 cm. Find the diameter of John's ball. - Skiing meeting
 Four friends came to the skiing meeting from 4 world directions and led the next interview. Charles: "I did not come from the north or from the south." Mojmir: "But I came from the south." Joseph: "I came from the north." Zdeno: "I come from the south." W
Four friends came to the skiing meeting from 4 world directions and led the next interview. Charles: "I did not come from the north or from the south." Mojmir: "But I came from the south." Joseph: "I came from the north." Zdeno: "I come from the south." W - Z9-I-4
 Kate thought of a five-digit integer. She wrote the sum of this number and its half in the first line of the workbook. Write a total of this number and its fifth on the second line. She wrote a sum of this number and its one nines on the third row. Finall
Kate thought of a five-digit integer. She wrote the sum of this number and its half in the first line of the workbook. Write a total of this number and its fifth on the second line. She wrote a sum of this number and its one nines on the third row. Finall - Tunnels
 Mice had built an underground house consisting of chambers and tunnels: • each tunnel leading from the chamber to the chamber (none is blind) • from each chamber lead just three tunnels into three distinct chambers, • from each chamber, mice can get to an
Mice had built an underground house consisting of chambers and tunnels: • each tunnel leading from the chamber to the chamber (none is blind) • from each chamber lead just three tunnels into three distinct chambers, • from each chamber, mice can get to an - Fluid
 We have vessels containing 7 liters, 5 liters, and 2 liters. The largest container is filled with fluid, and the others are empty. Can you only get 5 liters and two 1 liter of fluid by pouring? How much pouring is needed?
We have vessels containing 7 liters, 5 liters, and 2 liters. The largest container is filled with fluid, and the others are empty. Can you only get 5 liters and two 1 liter of fluid by pouring? How much pouring is needed? - Pet store
 They sold fish from one aquarium from the breeding product (Zverimex). Ondrej wanted half of all the fish, but to avoid cutting any fish, he got half the fish more than he wanted. Matej wanted half of the remaining fish, but like Ondrej, he got half the f
They sold fish from one aquarium from the breeding product (Zverimex). Ondrej wanted half of all the fish, but to avoid cutting any fish, he got half the fish more than he wanted. Matej wanted half of the remaining fish, but like Ondrej, he got half the f - Connected 3457
 There are eight places in Budan, some of which are connected by roads. There is a gate at every point where the road leaves or enters the city. No two paths intersect or enter through the same entrance. The number of gates matches one of the numbers 5,15,
There are eight places in Budan, some of which are connected by roads. There is a gate at every point where the road leaves or enters the city. No two paths intersect or enter through the same entrance. The number of gates matches one of the numbers 5,15, - Cat show
 A total of ten exhibitors gathered at the long-haired cat show. It was exhibited in a rectangular room with two rows of tables, as shown. The cats were marked with different numbers from 1 to 10, and one cat sat on each table. Determine which cat was rate
A total of ten exhibitors gathered at the long-haired cat show. It was exhibited in a rectangular room with two rows of tables, as shown. The cats were marked with different numbers from 1 to 10, and one cat sat on each table. Determine which cat was rate - Mr. Zucchini
 Mr. Zucchini had a rectangular garden whose perimeter was 28 meters. The garden's area is filled with just four square beds, whose dimensions in meters are expressed in whole numbers. Determine what size could have a garden. Find all the possibilities and
Mr. Zucchini had a rectangular garden whose perimeter was 28 meters. The garden's area is filled with just four square beds, whose dimensions in meters are expressed in whole numbers. Determine what size could have a garden. Find all the possibilities and - Decide
 The rectangle is divided into seven fields. In each box, write just one of the numbers 1, 2, or 3. Mirek argues that it can be done so that the sum of the two numbers written next to each other is always different. Zuzana (Susan) instead argues that it is
The rectangle is divided into seven fields. In each box, write just one of the numbers 1, 2, or 3. Mirek argues that it can be done so that the sum of the two numbers written next to each other is always different. Zuzana (Susan) instead argues that it is - Eight blocks
 Dana had the task of saving the eight blocks of these rules: 1. Between two red cubes must be a different color. 2. Between two blue must be two different colors. 3. Between two green must be three different colors. 4. Between two yellow blocks must be fo
Dana had the task of saving the eight blocks of these rules: 1. Between two red cubes must be a different color. 2. Between two blue must be two different colors. 3. Between two green must be three different colors. 4. Between two yellow blocks must be fo - Hexagon - MO
 The picture shows the ABCD square, the EFGD square, and the HIJD rectangle. Points J and G lie on the side CD and are true |DJ|
The picture shows the ABCD square, the EFGD square, and the HIJD rectangle. Points J and G lie on the side CD and are true |DJ| - MO 2016 Numerical axis
 Cat's school uses a special numerical axis. The distance between the numbers 1 and 2 is 1 cm, the distance between the numbers 2 and 3 is 3 cm, between the numbers 3 and 4 is 5 cm, and so on, and the distance between the next pair of natural numbers is al
Cat's school uses a special numerical axis. The distance between the numbers 1 and 2 is 1 cm, the distance between the numbers 2 and 3 is 3 cm, between the numbers 3 and 4 is 5 cm, and so on, and the distance between the next pair of natural numbers is al - Internal angles
 The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det
The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det - Hexagons
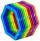 There is a square ABCD, a square EFGD, and a rectangle HIJD, points JG lie on the side CD, while DJ is less than DG, and points HE lie on the side DA, while DH is less than DE. We also know that DJ is equal to GC. Hexagon ABCGFE has a perimeter of 96 cm,
There is a square ABCD, a square EFGD, and a rectangle HIJD, points JG lie on the side CD, while DJ is less than DG, and points HE lie on the side DA, while DH is less than DE. We also know that DJ is equal to GC. Hexagon ABCGFE has a perimeter of 96 cm, - Soup
 On Monday, we cooked 25 pots and ten boilers of soup. On Tuesday, we cooked 15 pots and 13 boilers. On Wednesday, we cooked 20 pots, and on Thursday, we cooked 30 boilers. The same amount of soup was cooked on Monday and Tuesday. How many times is more so
On Monday, we cooked 25 pots and ten boilers of soup. On Tuesday, we cooked 15 pots and 13 boilers. On Wednesday, we cooked 20 pots, and on Thursday, we cooked 30 boilers. The same amount of soup was cooked on Monday and Tuesday. How many times is more so - MO - triangles
 On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a
On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
