Hexagon - MO
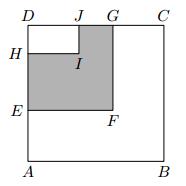
The picture shows the ABCD square, the EFGD square, and the HIJD rectangle. Points J and G lie on the side CD and are true |DJ| <|DG|, and the points H and E lie on the DA side, with the |DH| < |DE|. We also know that |DJ| = |GC|. The hexagon ABCGFE has a perimeter of 96 cm, the hexagon EFGJIH has a perimeter of 60 cm, and the rectangle HIJD has a perimeter of 28 cm. Find the area of the hexagon EFGJIH.
Final Answer:
You need to know the following knowledge to solve this word math problem:
geometryplanimetricsUnits of physical quantitiesthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Hexagons
There is a square ABCD, a square EFGD, and a rectangle HIJD, points JG lie on the side CD, while DJ is less than DG, and points HE lie on the side DA, while DH is less than DE. We also know that DJ is equal to GC. Hexagon ABCGFE has a perimeter of 96 cm, - Quadrilateral 66614
The picture shows a square ABCD with the center S and the side 8 cm long. Point E is any point on the CD side other than C and D. Calculate the area of the ASBE quadrilateral in cm². - Trapezoid thirds
The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment. - The rectangle 5
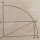The rectangle OABC has one vertex at O, the center of a circle, and a second vertex, A, 2 cm from the edge of the circle, as shown. The vertex A is also 7 cm from C. The points B and C lie on the circumference of the circle. a. What is the radius? b. Find - Rectangle and diagonal
In the rectangle ABCD, we know the side length is AB = 16 cm, and the diagonal AC = 20 cm. Calculate its perimeter and area. - Quadrilateral 80729
Quadrilateral ABCD has side lengths AB=13cm, CD=3cm, AD=4cm. Angles ACB and ADC are right angles. Calculate the perimeter of quadrilateral ABCD. - One trapezium
One trapezium has AB=24M, BC=36M, CD=80M, DA=80M long sides. Find the area.
