Šestiúhelník nepravidelný
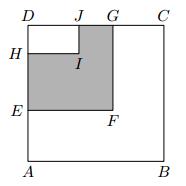
Na obrázku je čtverec ABCD, čtverec EF GD a obdélník HIJD. Body J a G leží na straně CD, přičemž platí |DJ| < |DG|, a body H a E leží na straně DA, přičemž platí |DH| < |DE|. Dále víme, že |DJ| = |GC|. Šestiúhelník ABCGFE má obvod 96 cm, šestiúhelník EF GJIH má obvod 60 cm a obdélník HIJD má obvod 28 cm.
Správná odpověď:
Zobrazuji 2 komentáře:
Mo-radce
Nápověda. Dokážete určit délku některé úsečky, aniž byste k tomu použili více než jeden zadaný rozměr?
Řešení.
Zjistíme rozměry čtverce EF GD a obdélníku HIJD, abychom stanovili jejich obsahy. Rozdíl těchto obsahů představuje žádaný obsah šestiúhelníku EFGJIH. Zadaný obvod šestiúhelníku EFGJIH je roven obvodu čtverce EFGD, neboť |JI| = |DH| a |HI| = |DJ|. Strana GD má tedy velikost 60 : 4 = 15 (cm). Podobně zadaný obvod šestiúhelníku ABCGF E je roven obvodu čtverce ABCD, velikost strany CD je tudíž 96 : 4 = 24 (cm). Rozdíl délek stran těchto dvou čtverců je roven délce úsečky GC, která je dle zadání rovna délce úsečky DJ:
|DJ| = |GC| = 24 − 15 = 9 (cm).
Pomocí známého obvodu obdélníku HIJD a délky strany DJ stanovíme i druhý rozměr tohoto obdélníku:
|JI| = (28 − 2 · 9) : 2 = 5 (cm).
Nyní máme všechny údaje potřebné ke stanovení obsahů čtverce EF GD a obdélníku HIJD:
S(EFGD) = 15 · 15 = 225 cm2
S(HIJD) = 9 · 5 = 45 cm2
Hledaný obsah šestiúhelníku tedy je S (EFGJIH) = 225 − 45 = 180 cm2.
Řešení.
Zjistíme rozměry čtverce EF GD a obdélníku HIJD, abychom stanovili jejich obsahy. Rozdíl těchto obsahů představuje žádaný obsah šestiúhelníku EFGJIH. Zadaný obvod šestiúhelníku EFGJIH je roven obvodu čtverce EFGD, neboť |JI| = |DH| a |HI| = |DJ|. Strana GD má tedy velikost 60 : 4 = 15 (cm). Podobně zadaný obvod šestiúhelníku ABCGF E je roven obvodu čtverce ABCD, velikost strany CD je tudíž 96 : 4 = 24 (cm). Rozdíl délek stran těchto dvou čtverců je roven délce úsečky GC, která je dle zadání rovna délce úsečky DJ:
|DJ| = |GC| = 24 − 15 = 9 (cm).
Pomocí známého obvodu obdélníku HIJD a délky strany DJ stanovíme i druhý rozměr tohoto obdélníku:
|JI| = (28 − 2 · 9) : 2 = 5 (cm).
Nyní máme všechny údaje potřebné ke stanovení obsahů čtverce EF GD a obdélníku HIJD:
S(EFGD) = 15 · 15 = 225 cm2
S(HIJD) = 9 · 5 = 45 cm2
Hledaný obsah šestiúhelníku tedy je S (EFGJIH) = 225 − 45 = 180 cm2.
9 let 1 Like
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometrieplanimetrieJednotky fyzikálních veličintémaÚroveň náročnosti úkolu
Související a podobné příklady:
- Šestiúhelníky
Je čtverec ABCD, čtverec EFGD a obdélnik HIJD, body JG leží na straně CD pričemž platí DJ je menší než DG a body HE leží na straně DA, pričemž platí DH je menší než DE, dále víme že DJ se rovná GC. Šestiúhelník ABCGFE má obvod 96 cm, šestiúhelník EFGJIH m - Rovnoramenný 2588
Daný je rovnoramenný lichoběžník ABCD, ve kterém platí |AB|= 2|BC|= 2|CD|= 2|DA|. Na jeho straně BC je bod K takový, že |BK| = 2|KC|, na jeho straně CD je bod L takový, že |CL|= 2|LD|, a na jeho straně DA je bod M takový, že|DM|= 2|MA|. Určete velikosti v - Trojúhelníku 63244
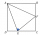Obsah Čtverce ABCD na obrázku je 36 cm². Jaký je v cm² obsah trojúhelníku AEF, pokud body E a F jsou středy stran čtverce BC a CD? - Čtyřúhelník ACEG
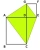Na obrázku jsou dva obdélníky ABCD a DEFG, přičemž |DE|=3 CM, |AD|=6 CM, |DG|= 5, |CD|= 10 CM. Vypočítejte obsah čtyřúhelníku ACEG. Popis obrázku: obdélníky mají společný jeden vrchol D. Obdélník ABCD má dvojnásobně dlouhé strany než DEFG. Všechny stranu - Čtyřúhelníku 81469
Dán je čtverec ABCD. Střed AB je E, střed BC je F, CD je G a střed DA je H. Spojíme AF, BG, CH a DE. Uvnitř čtverce (přibližně uprostřed) průsečíky těchto úseček vytvoří čtyřúhelník. Vypočítejte obsah tohoto čtyřúhelníku. Děkuji - Bod B
Bod B je vrchol obdélníku ABCD. Na přímce p leží úhlopříčka BD tohoto obdélníku. Bod X je vnitřní bod strany AD obdélníku ABCD a bod Y vnitřní bod strany CD. Sestrojte chybějící vrcholy D, A, C obdélníku ABCD. - Čtyřúhelníku 66614
Na obrázku je čtverec ABCD se středem S a stranou dlouhou 8 cm. Bod E je libovolný bod strany CD různé od C a D. Vypočítejte obsah čtyřúhelníku ASBE v cm².
