Hexagons
There is a square ABCD, a square EFGD, and a rectangle HIJD, points JG lie on the side CD, while DJ is less than DG, and points HE lie on the side DA, while DH is less than DE. We also know that DJ is equal to GC. Hexagon ABCGFE has a perimeter of 96 cm, hexagon EFGJIH has a perimeter of 60 cm and rectangle HIJD has a perimeter of 28 cm. Determine the area of hexagon EFGJIH.
Final Answer:
You need to know the following knowledge to solve this word math problem:
planimetricsbasic operations and conceptsthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Hexagon - MO
The picture shows the ABCD square, the EFGD square, and the HIJD rectangle. Points J and G lie on the side CD and are true |DJ| - Triangle angle operations
There are also two equilateral triangles ABC, and BDE, such that the size of the angle ABD is greater than 120° and less than 180° points C and E lie in the same half-plane defined by the line AD. The intersection of CD and AE is marked F. Determine the s - Rectangle and diagonal
In the rectangle ABCD, we know the side length is AB = 16 cm, and the diagonal AC = 20 cm. Calculate its perimeter and area. - Trapezoid angles
Given an isosceles trapezoid ABCD, in which | AB | = 2 | BC | = 2 | CD | = 2 | DA | holds. On its side BC, the point K is such that | BK | = 2 | KC |; on its CD side, the point L is such that | CL | = 2 | LD |, and on its DA side, the point M is such that - Quadrilateral perimeter angles
Quadrilateral ABCD has side lengths AB=13cm, CD=3cm, AD=4cm. Angles ACB and ADC are right angles. Calculate the perimeter of quadrilateral ABCD. - The rectangle 5
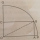The rectangle OABC has one vertex at O, the center of a circle, and a second vertex, A, 2 cm from the edge of the circle, as shown. The vertex A is also 7 cm from C. The points B and C lie on the circumference of the circle. a. What is the radius? b. Find - Circumscribed by triangle
Inside the rectangle ABCD, the points E and F lie so that the line segments EA, ED, EF, FB, and FC are congruent. Side AB is 22 cm long, and the circle circumscribed by triangle AFD has a radius of 10 cm. Determine the length of side BC.
