Mrak - cloud
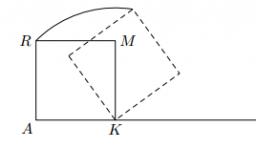
It is given segment AB, which is 12 cm in length, on which one side of the square MRAK is laid. MRAK's side length is 2 cm shown. MRAK gradually flips along the line segment AB, and point R leaves a paper trail.
Draw the whole track of point R until the square can do the line AB on both sides and returns to its original position.
Draw the whole track of point R until the square can do the line AB on both sides and returns to its original position.
Correct answer:
You need to know the following knowledge to solve this word math problem:
planimetricsthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Two chords
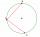There is a given circle k (center S, radius r). From point A, which lies on circle k, are starting two chords of length r. What angle do chords make? Draw and measure. - triangle 5420
Two pairs of parallel lines, AB to CD and AC to BD, are given. Point E lies on the line BD, point F is the midpoint of the segment BD, point G is the midpoint of the segment CD, and the area of the triangle ACE is 20 cm². Determine the area of triangl - Rhombus construction
Construct ABCD rhombus if its diagonal AC=9 cm and side AB = 6 cm. Inscribe a circle in it, touching all sides. - Trapezoid thirds
The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment.
- Divides 70604
Draw a point x on the line, which divides it in the given ratio: a) 2:3 b) 1:5 c) 6:2 - Calculate: 16973
The dragon is shaped like a diamond. Its diagonals are 60 cm and 90 cm long. Calculate: a) side of the rhombus b) how much paper do we need to make the kite? If we need to stick it on both sides, it needs 5% of the total area of the paper to bend. - Intersection 7247
On side AB of triangle ABC, points D and E are given such that |AD| = |DE| = |EB|. Points A and B are the midpoints of segments CF and CG. Line CD intersects line FB at point I, and line CE intersects line AG at point J. Prove that the intersection of lin
