Mathematical Olympiad - practice problems - page 7 of 9
Number of problems found: 176
- Pyramid Z8–I–6
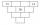Each brick of the pyramid contains one number. Whenever possible, the number in each brick is the lowest common multiple of two numbers of bricks lying directly above it. May that number be in the lowest brick? Determine all possibilities. - Celebration 4461
Anička has 50 CZK, Anežka has 46 CZK, and they want to use all the money to buy desserts for a family celebration. They decide between cakes and pinwheels. A pinwheel is CZK 4 more expensive than a cake, and for all the money, you could buy a third more c - Expression 4451
Find the largest natural number d that has that property for any natural number n; the number V(n) is the value of the expression: V (n) = n ^ 4 + 11n²−12 is divisible by d. - Coefficients 4445
Find all triplets P (x) = a * x² + b * x + c with the integer coefficients a, b, and c to which it applies P (1) - Inequality 4434
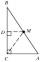The heel of height from the vertex C in the triangle ABC divides the side AB in the ratio 1:2. Prove that in the usual notation of the lengths of the sides of the triangle ABC, the inequality 3 | a-b | holds - Shopkeeper 4433
The seller of Christmas trees sold spruces for 220 CZK, pines for 250 CZK, and hemlocks for 330 CZK. In the morning he had an equal number of spruces, hemlocks, and pines. In the evening, he had sold all the trees and received a total of 36,000 CZK for th - MO-I-Z6
A square with a side of 4 cm is divided into squares with a side of 1 cm as shown in the figure. Divide the square along the marked lines into two figures with a perimeter of 16 cm. Find at least three different solutions (i.e. three such solutions that n
- Isosceles - isosceles
It is given a triangle ABC with sides /AB/ = 3 cm /BC/ = 10 cm, and the angle ABC = 120°. Draw all points X such that the BCX triangle is an isosceles and triangle ABX is an isosceles with the base AB. - Trapezoid MO-5-Z8
ABCD is a trapezoid in that lime segment CE is divided into a triangle and parallelogram. Point F is the midpoint of CE, the DF line passes through the center of the segment BE, and the area of the triangle CDE is 3 cm². Determine the area of the trapezoi - Cakes Z8-I-5
Mom brought ten cakes of three types: coconut was less than Meringue Cookies, and most were caramel cubes. John chose two different kinds of cakes. Stephan did the same, and Margerith left only the same type of cake. How many coconuts, Meringue Cookies an - Four families
Four families were on a joint trip. The first family had three siblings: Alica, Betka, and Cyril. In the second family were four siblings: David, Erik, Filip, and Gabika. In the third family, there were two siblings, Hugo and Iveta. Three siblings in the - Star equation
Write digits instead of stars so that the sum of the written digits is odd and is true equality: 42 · ∗8 = 2 ∗∗∗ - Centipede Mira
Centipede Miroslava consists of a head and several articles. Each pair has one pair of legs. When it got cold, she decided to get dressed. Therefore, she put a sock on her left foot from the end of the third article and then in every other third article. - Christmas trees
The salesman sold Christmas trees: spruce for € 22, pine for € 25, and fir for € 33. In the morning, he had the same number of spruce, fir, and pine. In the evening, he had all the trees sold for € 3,600. How many trees does the day salesman sell? - MO-Z5-3-66 tiles
The picture shows square tiles with a side of 10 dm, composed of four identical small rectangles and squares. The circumference of a small square is five times smaller than the circumference of the entire tile. Determine the dimensions of the rectangle.
- Take a photo
Four boys are living in a three-story house. Each lives on a different floor. We know this about them: - Josef is a philatelist - Viktor does not live on the top floor and cannot take photographs - Ivan is friends with an amateur photographer from the gro - Candy - MO Gretel deploys different numbers to the vertex of a regular octagon, from one to eight candy. Peter can then choose which three piles of candy to give Gretel others retain. The only requirement is that the three piles lie at the vertices of an isosceles t
- Octahedron - sum
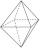On each wall of a regular octahedron is written one of the numbers 1, 2, 3, 4, 5, 6, 7, and 8, wherein on different sides are different numbers. John makes the sum of the numbers written on three adjacent walls for each wall. Thus got eight sums, which al - Three friends
Three friend squirrels together went to collect hazelnuts. Zrzecka found more than twice Pizizubka, and Ouska was even three times more than Pizizubka. On the way home, they talked while eating and cracked her nuts. Pizizubka ate half of all the nuts coll - Z9–I–1
All nine fields of given shape are to be filled with natural numbers so that: • each of the numbers 2, 4, 6, and 8 is used at least once, • four of the inner square boxes containing the products of the numbers of adjacent cells of the outer square, • in t
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
See also more information on Wikipedia.
