Trapezoid MO-5-Z8
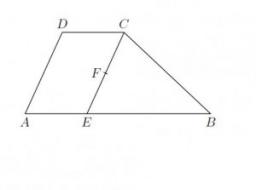
ABCD is a trapezoid that lime segment CE is divided into a triangle and parallelogram, as shown. Point F is the midpoint of CE, DF line passes through the center of the segment BE, and the area of the triangle CDE is 3 cm2.
Determine the area of the trapezoid ABCD.
Determine the area of the trapezoid ABCD.
Correct answer:
Tips for related online calculators
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Rhombus construction
Construct ABCD rhombus if its diagonal AC=9 cm and side AB = 6 cm. Inscribe a circle in it touching all sides... - Trapezoid thirds
The ABCD trapezoid with the parallel sides of the AB and the CD and the E point of the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment. - Diagonal intersect
Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles? - Triangle 69144
The line p passes through the center of gravity T of the triangle and is parallel to the line BC. What is the ratio of the area of the divided smaller part of the triangle by the line p and the area of the triangle? - Right triangle from axes
A line segment has its ends on the coordinate axes and forms with them a triangle of area equal to 36 square units. The segment passes through the point ( 5,2). What is the slope of the line segment? - Internal angles
The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det - MO Z8–I–6 2018
In the KLMN trapeze, KL has a 40 cm base and an MN of 16 cm. Point P lies on the KL line so that the NP segment divides the trapezoid into two parts with the same area. Find the length of the KP line. - Katy MO
Kate drew triangle ABC. The middle of the line segment AB has marked as X and the center of the side AC as Y. On the side BC she wants to find the point Z such that the area of a 4gon AXZY was greatest. What part of the triangle ABC can maximally occupy 4 - Trapezoid 4908 Trapezoid ABCD with bases AB = a, CD = c has height v. The point S is the center of the arm BC. Prove that the area of the ASD triangle is equal to half the area of the ABCD trapezoid.
- Circle and square
An ABCD square with a side length of 100 mm is given. Calculate the radius of the circle that passes through the vertices B, C and the center of the side AD. - Center
In the ABC triangle is point D[1,-2,6], which is the center of the |BC|, and point G[8,1,-3], which is the center of gravity of the triangle. Find the coordinates of the vertex A[x,y,z]. - Dividing rod
The 3m long rod should be divided into two parts so that one is 16cm longer than the other. Find the lengths of both parts. - Parallelogram
Calculate area of the parallelogram ABCD as shown if |AB| = 19 cm, |BC| = 18 cm and angle BAD = 90° - Diagonal in rectangle
In that rectangle ABCD is the center of BC point E and point F is center of CD. Prove that the lines AE and AF divide diagonal BD into three equal parts. - Line
Write an equation of a line parallel to To 9x + 3y = 8 That Passes Through The Point (-1, -4). Write in form ax+by=c. - KLMN trapezoid The KLMN trapezoid has bases KL 40cm and MN 16cm. On the KL base is point P. The segment NP divides the trapezoid into units with the same area. What is the distance of point P from point K?
- Coordinates
Determine the coordinates of the vertices and the area of the parallelogram, the two sides of which lie on the lines 8x + 3y + 1 = 0, 2x + y-1 = 0 and the diagonal on the line 3x + 2y + 3 = 0
