Trapezoid 83
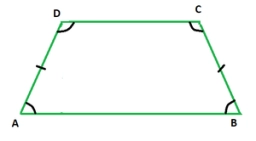
Trapezoid ABCD is composed of five triangles. Points E, and G divide segment AB in the ratio 2:4:3 (in this order) into three segments. Point F is the midpoint of segment AD. Triangle AEF is isosceles and right-angled. Triangles GBC and CDG are right-angled. The area of triangle AEF is 8cm2. What is the perimeter of the trapezoid?
Final Answer:
Tips for related online calculators
Check out our ratio calculator.
Do you want to convert length units?
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
Do you want to convert length units?
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryalgebraarithmeticplanimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- MO - triangles
 On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a
On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a - Diagonal intersect
 Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles?
Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles? - Triangle ABP
 An isosceles trapezoid ABCD is given. The length of side AB is 10 cm, the length of CD is 7 cm, and the height to side AB is 4 cm. Point P is the base of the altitude to side AD. Calculate the area of the triangle ABP.
An isosceles trapezoid ABCD is given. The length of side AB is 10 cm, the length of CD is 7 cm, and the height to side AB is 4 cm. Point P is the base of the altitude to side AD. Calculate the area of the triangle ABP. - Segment ratio division
 AB segment = 14 cm, divide it into two segments whose lengths are in the ratio 4:3.
AB segment = 14 cm, divide it into two segments whose lengths are in the ratio 4:3. - Trapezoid MO-5-Z8
 ABCD is a trapezoid in that lime segment CE is divided into a triangle and parallelogram. Point F is the midpoint of CE, the DF line passes through the center of the segment BE, and the area of the triangle CDE is 3 cm². Determine the area of the trapezoi
ABCD is a trapezoid in that lime segment CE is divided into a triangle and parallelogram. Point F is the midpoint of CE, the DF line passes through the center of the segment BE, and the area of the triangle CDE is 3 cm². Determine the area of the trapezoi - Coat of arms
 The class created its coat of arms, which had a shape composed of an isosceles trapezoid ABCD (shorter base is a = 4.5 cm long, longer 2a = 9 cm, trapezoid height 6 cm) and a semicircle with center S and diameter AB. Three identical isosceles triangles fo
The class created its coat of arms, which had a shape composed of an isosceles trapezoid ABCD (shorter base is a = 4.5 cm long, longer 2a = 9 cm, trapezoid height 6 cm) and a semicircle with center S and diameter AB. Three identical isosceles triangles fo - Rectangular trapezoid
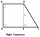 The ABCD rectangular trapezoid with the AB and CD bases is divided by the diagonal AC into two equilateral rectangular triangles. The length of the diagonal AC is 62cm. Calculate the trapezium area in cm square and calculate how many different perimeters
The ABCD rectangular trapezoid with the AB and CD bases is divided by the diagonal AC into two equilateral rectangular triangles. The length of the diagonal AC is 62cm. Calculate the trapezium area in cm square and calculate how many different perimeters
