Coat of arms

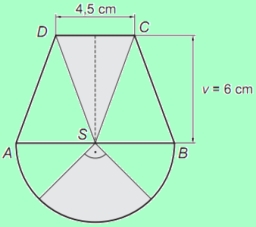
The class created its coat of arms, which had a shape composed of an isosceles trapezoid ABCD (shorter base is a = 4.5 cm long, longer 2a = 9 cm, trapezoid height 6 cm) and a semicircle with center S and diameter AB. Three identical isosceles triangles formed the trapezoid. Pupils painted the semicircle's gray half and the trapezoid's middle field (central triangle). How many cm² areas of the coat of arms were gray? Please round the result to one decimal place.

Final Answer:

S =  29.4 cm²

Step-by-step explanation:

$$\begin{gathered} a=4.5\text{cm} \\ c=2\cdot a=2\cdot 4.5=9\text{cm} \\ v=6\text{cm} \\ r=a=4.5=\frac{9}{2}=4.5\text{cm} \\ {S}_1=\frac{a+c}{2}\cdot v=\frac{4.5+9}{2}\cdot 6=\frac{81}{2}=40.5{\text{cm}}^2 \\ {S}_2=\pi \cdot r^2/2=3.1416\cdot 4.5^2/2\doteq 31.8086{\text{cm}}^2 \\ S=S_1/3+S_2/2=40.5/3+31.8086/2=29.4{\text{cm}}^2 \end{gathered}$$

Try another example