The bases

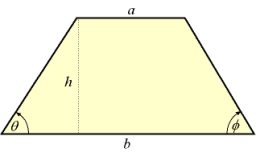
The bases of the isosceles trapezoid ABCD have lengths of 10 cm and 6 cm. Its arms form an angle α = 50˚ with a longer base. Calculate the circumference and content of the ABCD trapezoid.

Correct answer:

o =  22.2229 cm
S =  19.0681 cm²

Step-by-step explanation:

$$\begin{gathered} a=10\text{ cm } \\ c=6\text{ cm } \\ \alpha =50\text{ ° } \\ x=(a-c)\mathrm{/}2=(10-6)\mathrm{/}2=2\text{ cm } \\ \cos \alpha =x:r \\ r=x\mathrm{/}\cos (\alpha )=2\mathrm{/}\cos (50\mathrm{°})=3.11145\text{ cm } \\ o=a+c+2\cdot r=10+6+2\cdot 3.1114=22.2229\text{ cm} \end{gathered}$$

$$\begin{gathered} \tan \alpha =h:x \\ h=x\cdot \tan (\alpha )=2\cdot \tan (50\mathrm{°})=2.38351\text{ cm } \\ S={\displaystyle \frac{a+c}{2}}\cdot h={\displaystyle \frac{10+6}{2}}\cdot 2.3835=19.0681{\text{cm}}^2 \end{gathered}$$

Try another example

Related math problems and questions:

• Land - isosceles trapezoid
  Calculate the building plot's content and perimeter in the form of an isosceles trapezoid with bases 120m, 95m, and height 50m.
• Ratio in trapezium
  The height v and the base a, c in the trapezoid ABCD are in the ratio 1: 6: 3, its content S = 324 square cm. Peak angle B = 35 degrees. Determine the perimeter of the trapezoid
• Isosceles trapezoid
  The lengths of the bases of the isosceles trapezoid are in the ratio 5:3, the arms have a length of 5 cm and height = 4.8 cm. Calculate the circumference and area of a trapezoid.
• Isosceles triangle
  Calculate area and perimeter of an isosceles triangle ABC with base AB if a = 6 cm, c = 7 cm.
• ISO trapezoid v2
  bases of Isosceles trapezoid measured 20 cm and 4 cm and its perimeter is 55 cm. What is the are of a trapezoid?
• Isosceles trapezoid
  Find the height in an isosceles trapezoid if the area is 520 cm² and the base a = 25 cm and c = 14 cm. Calculate the interior angles of the trapezoid.
• Isosceles
  Isosceles trapezium ABCD ABC = 12 angle ABC = 40 ° b=6. Calculate the circumference and area.
• Diagonal
  The rectangular ABCD trapeze, whose AD arm is perpendicular to the AB and CD bases, has an area of 15 cm square. Bases have lengths AB = 6cm, CD = 4cm. Calculate the length of the AC diagonal.
• Right triangle
  It is given a right triangle angle alpha of 90 degrees beta angle of 55 degrees c = 10 cm use Pythagorean theorem to calculate sides a and b
• Isosceles trapezium
  Calculate the area of an isosceles trapezium ABCD if a = 10cm, b = 5cm, c = 4cm.
• Isosceles trapezoid
  Find the area of an isosceles trapezoid, if the bases are 12 cm and 20 cm, the length of the arm is 16 cm
• Right triangle
  Calculate the missing side b and interior angles, perimeter, and area of ​​a right triangle if a=10 cm and hypotenuse c = 16 cm.
• Isosceles trapezoid
  Calculate the content of an isosceles trapezoid whose bases are at ratio 5:3, the arm is 6cm long and it is 4cm high.
• Arm and base
  The isosceles triangle has a circumference of 46 cm. Calculate its area if the arm is 5 cm longer than the base.
• Roof angle
  The roof of the house has the shape of an isosceles triangle with arms 4 m long and the size of the base 6 m. How big an angle alpha does its roof make?
• Isosceles triangle
  Calculate the area of an isosceles triangle, the base of which measures 16 cm and the arms 10 cm.
• Parallelogram ABCD
  We have the parallelogram ABCD, where AB is 6.2 cm BC is 5.4 cm AC is 4.8 cm calculate the height on the AB side and the angle DAB