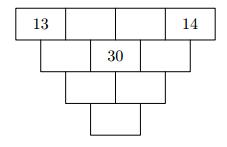
Pyramid Z8–I–6
Each brick of the pyramid contains one number. Whenever possible, the number in each brick is the lowest common multiple of two numbers of bricks lying directly above it.
May that number be in the lowest brick? Determine all possibilities.
May that number be in the lowest brick? Determine all possibilities.
Final Answer:
Tips for related online calculators
Do you want to calculate the least common multiple of two or more numbers?
You need to know the following knowledge to solve this word math problem:
algebrabasic operations and conceptsthemes, topicsGrade of the word problem
Related math problems and questions:
- Four classses
Students of all 7, 8, and 9 classes in one school may take up 4, 5, 6, and 7 abreast, and nobody will be left. If there are always four classes in each grade, what is the average number of pupils in one class? - Purchased
Milan shopped in a store where the prices of all goods were listed in whole €. If Milan bought 2 milk, 3 glasses, and 1 pack of sweets, he would pay €49. If he bought 5 more milks, 11 glasses, and 1 pack of sweets, he would pay a total of €154. How much € - Brick
The isosceles scale has all bricks; the second weight is 1 kg, and the 1/5 of brick is on one side. The balance is in equilibrium. What is the weight of a brick? - Digits
How many odd four-digit numbers can we create from digits 0, 3, 5, 6, and 7? (a) the figures may be repeated (b) the digits may not be repeated - Unknown number
An unknown number is divisible by exactly three different primes. When we compare these primes in ascending order, the following applies: • The difference between the first and second prime numbers is half the difference between the third and second prime - Toy choices
Adamko is two years old and does not want to clean his toys. One night, the toy fairy came to his room and saw legos, a police car, blocks, and a train lying on the floor. The fairy decided to take 3 toys from Adamko. How many choices does a trio of toys - Majorette rows
During a public performance, majorettes line up in three-step, four-step, six-step, and eight-step. All rows are full with each grouping, and no majorette is promoted. Determine the smallest possible number of majorettes for which a performance can be mad
