Mathematical Olympiad - practice problems - page 6 of 9
Number of problems found: 176
- Remaining 5534
On the table lay eight cards with the numbers 2,3,5,7,11,13,17,19. Fero chose three cards. He added the numbers written on them and found that their sum was 1 more than the sum of the numbers on the remaining cards. Which cards could have been left on the - Three-digit 5524
Six cards with digits 1, 2, 3, 4, 5, and 6 are on the table. Agnes made a six-digit number from these cards, divisible by six. Then she gradually removed the cards from the right. A five-digit number divisible by five remained on the table when she remove - Circumscribed by triangle
Inside the rectangle ABCD, the points E and F lie so that the line segments EA, ED, EF, FB, and FC are congruent. Side AB is 22 cm long, and the circle circumscribed by triangle AFD has a radius of 10 cm. Determine the length of side BC. - Z9–I–4 MO 2017
Numbers 1, 2, 3, 4, 5, 6, 7, 8, and 9 were prepared for a train journey with three wagons. They wanted to sit out so that three numbers were seated in each carriage, and the largest of the three was equal to the sum of the remaining two. The conductor sai - Candies - coloured
There were red and green candies in the tin. Čenek ate 2/5 of all the red candies, and Zuzka ate 3/5 of all the green candies. Now, the red candies make up 3/8 of all the candies in the can. How many candies were originally in the can? - triangle 5420
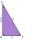Two pairs of parallel lines, AB to CD and AC to BD, are given. Point E lies on the line BD, point F is the midpoint of the segment BD, point G is the midpoint of the segment CD, and the area of the triangle ACE is 20 cm². Determine the area of triangl - Intersection of the altitudes
In the acute triangle KLM, the angle KLM is 68°. Point V is the intersection of the altitudes, and P is the foot of the altitude on the side LM. The angle P V M axis is parallel to the side KM. Compare the sizes of angles MKL and LMK.
- Double-digit 5411
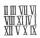Anička and Blanka each wrote one double-digit number, which started with a seven. The girls chose different numbers. Then, each inserted a zero between the two digits, giving them a three-digit number. Everyone subtracted their original two-digit number f - MO Z6-I-2 2017
Erika wanted to offer chocolate to her three friends. When she took it out of her backpack, she found that it was broken, as shown in the picture. (The marked squares are identical.) The girls have agreed not to break the chocolate anymore and will draw l - Adela number
Adela had two numbers written on the paper. When she added their greatest common divisor and least common multiple, she was given four different numbers less than 100. She was amazed that if she divided the largest of these four numbers by the least, she - Average age
The average age of all people at the celebration was equal to the number of people present. After the departure of one person who was 29 years old, the average age was again equal to the number present. How many people were original to celebrate? - Something 5385
Janko got pocket money and wants to buy something good for it. If he purchased four cakes, it would increase by 0.50 euros. If he wanted to buy five cakes, he would miss 0.60 euros. He would spend all his pockets on the rest if he bought two cakes and thr - MO8-Z8-I-5 2017
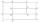Identical rectangles ABCD and EFGH are positioned such that their sides are parallel to the same. The points I, J, K, L, M, and N are the intersections of the extended sides, as shown. The area of the BNHM rectangle is 12 cm2, the rectangle MBC - One million
Write the million number (1000000) using only nine numbers and algebraic operations plus, minus, times, divided, powers, and squares. Find at least three different solutions. - Participants 5319 In the mathematical competition, its participants solved two tasks. Everyone solved at least one problem, while 80% of the participants solved the first problem, and 50% solved the second problem. Sixty participants solved both tasks. How many participant
- Three-digit 5312 Find the smallest four-digit number abcd such that the difference (ab)²− (cd)² is a three-digit number written in three identical digits.
- Alarm clock
The old watchmaker has a unique digital alarm in its collection that rings whenever the sum of the alarm's digits equals 21. Find out when the alarm clock will ring. What is their number? List all options. - Bicycles
You're the owner of the transport's learning playground. Buy bicycles of two colors, but you've got to spend accurately 120000 CZK. The Blue bike costs 3600 CZK and the red bicycle 3200 CZK. - MO Z6-6-1
Write integers greater than 1 to the blanks in the following figure so that each darker box is a product of the numbers in the neighboring lighter boxes. What number is in the middlebox? - Z7-I-4 stars 4949
Write instead of stars digits, so the next write of the product of the two numbers is valid: ∗ ∗ ∗ · ∗ ∗ ∗ ∗ ∗ ∗ ∗ 4 9 4 9 ∗ ∗ ∗ ∗ ∗ ∗ 4 ∗ ∗
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
See also more information on Wikipedia.
