Mathematical Olympiad - practice problems - page 5 of 9
Number of problems found: 176
- Definitely 7179
Ivan and Mirka shared pears in the mission. Ivan always takes two pears, and Mirka takes half of what remains in the mission. Thus, Ivan, Mirka, Ivan, Mirka, and finally Ivan, who took the last two pears, took them away. Definitely. Who had more pears, in - MO C–I–1 2018
An unknown number is divisible by just four numbers from the set {6, 15, 20, 21, 70}. Determine which ones. - Mathematical 7136
Out of 50 pupils, 44 solved at least one of the Olympiads - MO Mathematical Olympiad and BO Biology Olympiad. Twenty pupils still need to solve the MO. Of those who dealt with both Olympiads, 1/3 of those who dealt with just one were. How many pupils solv - Bedrich and Adam
When Bedrich is as old as Adam today, Adam will be 14 years old. When Adam was as old as Bedrich, Bedrich was two years old today. How old are Adam and Bedrich today? - MO Z8-I-1 2018 Fero and David meet daily in the elevator. One morning, they found that if they multiply their current age, they get 238. If they did the same after four years, this product would be 378. Determine the sum of the current ages of Fero and David.
- Together 7114
Michaella has five crayons. Victor has fewer of them than Michaella. Vendelín has as many as Michaella and Vojto have together. All three have seven times more crayons than Victor. How many crayons does Vendelín have? - Clubhouse
There were only chairs and tables in the clubhouse. Each chair had four legs, and the table was triple. Scouts came to the clubhouse. Everyone sat on their chair, two chairs were left unoccupied, and the number of legs in the room was 101. How many chairs
- Interested 7090
We call a natural number N bombastic if it contains no zero in its notation and if no smaller natural number has the same product of digits as the number N. Charles first became interested in bombastic prime numbers and claimed that there were not many of - Sufficiently 7059
The king gave the mason Václav the task of building a wall 25 cm thick, 50 m long, and 2 m high. If Václav had worked without a break and at the same pace, he would have built a wall in 26 hours. However, according to the valid royal regulations, Wencesla - MO Z8–I–6 2018
The KLMN trapezium, KL has a 40 cm base and an MN of 16 cm. Point P lies on the KL line so that the NP segment divides the trapezoid into two parts with the same area. Find the length of the KP line. - Positive 7040
Find all positive integers x and y for which: 1 / x + 1 / y = 1/4 - Manufacturer 6981
The hotelier wanted to equip the dining room with new chairs. He chose the type of chair in the catalog. Only when placing an order did he learn from the manufacturer that they offered every fourth chair at half price as part of the discount offer and tha - Equilateral triangle ABC
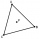In the equilateral triangle ABC, K is the center of the AB side, the L point lies on one-third of the BC side near point C, and point M lies on one-third of the side of the AC side closer to point A. Find what part of the ABC triangle contains the triangl - Last digit What is the last number of 2016 power of 2017
- Circumference 6598
Adam had three identical rectangles. He put them together and got a rectangle with a circumference of 50 cm. Then, he placed them differently and got a rectangle with a larger circumference. Calculate its perimeter.
- Kilometers 6417
It is 16 km from point A to B. from point C to B, it is 20 km from point C to D, it is 19 km how many kilometers is it from point D to point A - Determine 5893
Determine the largest integer n for which the square table n×n can be filled with natural numbers from 1 to n² (n squared) so that at least one square power of the integer is written in each of its 3×3 square parts. - Different 5874
Mišo and Rišo ran back and forth on the running track. They started towards each other, each from a different end of the track. Both were still running at the same speed, each at a different speed. The first time, they met 800 m from one end of the track, - 3N on the number axis
The line represents the number axis, and the marked points correspond to the numbers a, - a, and a + 1, but in no particular order. Construct the points that correspond to the numbers 0 and 1. Discuss all the possibilities. - Corresponding 5585
Consider the various points corresponding to the numbers a, 2a, 3a + 1 in all possible orders on the straight line representing the number line. For each option, decide whether such an arrangement is possible. If yes, give a specific example; if not, give
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
See also more information on Wikipedia.
