MO Z8–I–6 2018
The KLMN trapezium, KL has a 40 cm base and an MN of 16 cm. Point P lies on the KL line so that the NP segment divides the trapezoid into two parts with the same area. Find the length of the KP line.
Your answer:
Your answer:
Tips for related online calculators
Looking for help with calculating arithmetic mean?
Looking for a statistical calculator?
See also our trigonometric triangle calculator.
Looking for a statistical calculator?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
statisticsarithmeticplanimetryUnits of physical quantitiesthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- KLMN trapezoid
The KLMN trapezoid has bases KL 40 cm and MN 16 cm. On the KL base is point P. The segment NP divides the trapezoid into units with the same area. What is the distance of point P from point K? - Trapezoid thirds
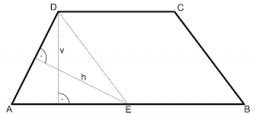
The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment. - Two points
M and N are two points on the X-axis and Y-axis, respectively. Point P (3, 2) divides the line segment MN in a ratio of 2:3. Find: (i) the coordinates of M and N (ii) slope of the line MN. - Line division calculation
The KL line is 12 cm long. Point X divides the line in a ratio of 1:5. What is the length of line XL if point X is closer to point K? - KLMN
In the KLMN trapezoid is given this information: 1. segments KL and MN are parallel 2. segments KL and KM have the same length 3. segments KN, NM, and ML have the same length. Determine the size of the angle KMN. - Dividing rod
The 3 m long rod should be divided into two parts so that one is 16 cm longer than the other. Find the lengths of both parts. - Internal angles
The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det
