Determine 5893
Determine the largest integer n for which the square table n×n can be filled with natural numbers from 1 to n2 (n squared) so that at least one square power of the integer is written in each of its 3×3 square parts.
Final Answer:
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsbasic operations and conceptsnumbersthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Z9–I–1
All nine fields of given shape are to be filled with natural numbers so that: • each of the numbers 2, 4, 6, and 8 is used at least once, • four of the inner square boxes containing the products of the numbers of adjacent cells of the outer square, • in t - Smallest 4692
A. Find the largest natural number by which the numbers 54 and 72 can be divided (120, 60, and 42) B. Find the smallest natural number that can be divided by each of the numbers 36 and 48 (24,18 and 16) - Perfect cube
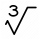Which of the following numbers is not a perfect cube? a. 64 b. 729 c. 800 d. 1331 - Decide
The rectangle is divided into seven fields. In each box, write just one of the numbers 1, 2, or 3. Mirek argues that it can be done so that the sum of the two numbers written next to each other is always different. Zuzana (Susan) instead argues that it is - Cube from sphere
What largest surface area (in cm²) can have a cube that we cut out of a sphere with a radius 26 cm? - Twenty
Twenty rabbits are put in 4 cells so that there are a different number of rabbits in each cell containing at least three rabbits. What is the largest possible number of rabbits in one cell? - Four-sevenths 34451
In how many parts do I have to divide the line whose endpoints are the images of the numbers 0 and 1 on the number axis so that they can be displayed: three-fifths, four-sevenths, five-eighths, and six-sixths
