Natural numbers - practice problems

Natural numbers are all positive integers from 1 to infinity. They are also called counting numbers as they are used to count objects. Zero is not natural number. It is represented by numerals as 1,2,3.... 8, ..., etc.

Number of problems found: 1826

Make a number
How can 8,2,5, and 6 make 24?
Divide 46
Divide 1111 in the ratio of 8:3 .
The remainder
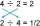Write the remainder as a fraction of 364 divided by 16
Six eggs
I have six eggs. I broke two. I fry two and I eat two. How many is left? What is the answer?
Divide 37
Divide 2406 cherries equally among 3 children. How many each got?
Evaluate 36
If a = 8 and b = 4, evaluate the following expression: 2 a − 3 b
The Three Little Pigs
Mary had 3 pigs and gave 1 pig to Will. How many pigs did Mary stay?
Dividend, divisor and quotient
Hiba got the answer of 72 after dividing two numbers. If the divisor was 14, what was the dividend?
50 people
Fifty people went to a play. 3/5 of the people stayed until the end. How many people are left?
Pants
Peter bought 58 pairs of pants, 18 of which were torn. How many pants were not torn, which he had?
Maddie
Maddie has 180 coins. Of these coins, 1/12 are dimes. About how many dimes does she have?
Cakes 6
If each of the 7 cakes is cut into eighths, how many pieces will be there?
In Paris
In Paris, TX, there are approximately 25,000 people. Of those people, 1/4 are under the age of 18. How many people are under the age of 18?
You have 3
You have the numbers 4,2, and 8. Use the numbers to make a calculation so that the answer is 40=
Two numbers 16
Two numbers are added together to give a sum of 1492. if one of the numbers is 821, what is the other number?
The ratio 18
The ratio of dogs to cats at a shelter is 2 to 7. If there are 12 dogs, then how many cats are in the shelter?
Pictures cards
Tom had 25 picture cards. He gave 2/5 of them to his friends. How many cards did Tom give to his friends?
The room temperature
At 5 AM, the room temperature was 20 degrees Celsius. After 6 hours, the reading was 28 degrees Celsius. The temperature rose by how many degrees?
The bouquets
A wedding planner is making bouquets. She must have equal numbers of bouquets made of 7 and 10 balloons each. How many bouquets would she get from 85 balloons?
There 34
There were 90 children at the birthday party. If 3/5 of them were boys, how many were girls?

Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.