Matematická olympiáda - príklady
Úlohy MO nie sú ľahké, ani pre dospelých ľudí. Zároveň veríme, že správne riešenie, ktoré je tu publikované takmer na jeden klik poslúži na len inšpiráciu. V reálnom živote každý totiž rieši úlohy, ktoré nikto iný pred tým neriešil.Nenechajte sa odradiť, keď neobjavíte hneď riešenie. Experimentujte, kreslite si, ”hrajte sa“ s úlohou. Niekedy pomôže pozrieť sa do nejakej knižky, kde nájdete podobné úlohy vyriešené, inokedy sa môže stať, že zrazu o tri dni ”z ničoho nič“ na riešenie prídete.
Počet nájdených príkladov: 206
- Dohromady 84159
Andulka a Zuzana pojedali slivky. Prvý deň zjedla Andulka tri štvrtiny toho, čo v ten istý deň zjedla Zuzana. Druhý deň zjedla Zuzana tri polovice toho, čo v ten istý deň zjedla Andulka. Dohromady za oba dni zjedli 31 sliviek a každé dievča každý deň zjed - Ciferný MO z9-I-4
Rozhodnite, či je možné k číslu s ciferným súčtom 2024 pripočítať jednociferné číslo tak, aby výsledné číslo malo ciferný súčet 74. - V obdĺžniku 2
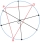V obdĺžniku so stranami dĺžok 4cm a 8cm ležia dve rôzne polkružnice, z ktorých každá má krajné body v jeho susedných vrcholoch a dotýka sa protiľahlej strany. Zostrojte štvorec taký, že jeho dva vrcholy ležia na jednej polkružnici, zvyšné dva na druhej a - Trojuholníkov 83111
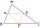Peťo zložil z navzájom zhodných trojuholníkov niekoľko rovinných útvarov. Obvody prvých troch sú postupne 8 cm, 11,4 cm a 14,7 cm. Určite obvod štvrtého útvaru
- Adam MO (asi MO Z8)
Adam napísal nasledujúci súčet s piatimi tajnými sčítancami: a + bb + ccc + dddd + eeeee. Prezradil, že znaky „a, b, c, d, e“ predstavujú navzájom rôzne cifry 1, 2, 3, 4, 5 a že výsledný súčet je deliteľný 11. Ktoré najmenšie a ktoré najväčšie číslo môž - Trojuholníka 82724
Pravouhlý trojuholník má obsah 36 cm². V ňom je umiestnený štvorec tak, že dve strany štvorca sú časťami dvoch strán trojuholníka a jeden vrchol štvorca je v tretine najdlhšej strany. Určite obsah tohto štvorca. - Mo z5 2023 psy
Anetkin strýko má narodeniny v rovnaký deň v roku ako Anetkin teta. Strýko je starší ako teta, nie však o viac ako o desať rokov, a obaja sú plnoletí. Na poslednej oslave ich narodenín si Anetka uvedomila, že keď vynásobí ich oslavované veky a výsledný sú - Trojuholník MO Z8-I-5
Trojuholník ABC je rozdelený úsečkami. Úsečky DE a AB sú rovnobežné. Trojuholníky CDH, CHI, CIE, FIH majú rovnaký obsah a to 8 dm². Zistite obsah štvoruholníka AFHD. - Zajac 2024m
Zajac sa zúčastnil na pretekoch dlhých 2024 metrov. Zo štartovej čiary sa odrazil ľavou nohou a po celý čas pretekov pravidelne striedal ľavú, pravú a obe nohy. Keď sa zajac odrazil ľavou nohou, skočil 35 dm, keď sa odrazil pravou nohou, skočil 15
- Karol 9 Karol mal vynásobiť dve dvojciferné čísla. Z nepozornosti vymenil poradie cifier v jednom z činiteľov a dostal súčin, ktorý bol o 4 248 menší ako správny výsledok. Aký je správny výsledok? Koľko malo Karolovi správne vyjsť?
- MO 2023
V záhradkarskej osade mal pán Jahoda vo svojom sude 16.litrov vody. Sused Malina mal vo svojom sude tri krát viac vody, ako pán Jahoda. Začalo pršať a do oboch sudov napršalo rovnaké množstvo vody. Po daždi pán Malina zistil, že má v sude dvakrát viac vod - Adam mal 3
Adam mal papier, ktorý bol natoľko veľký, že by sa z neho dalo natrhať niekoľko desiatok tisíc kúskov. Najprv papier roztrhal na štyri kúsky. Každý z týchto kú skov vzal a roztrhal buď na štyri, alebo na desať kúskov. Rovnakým spôsobom pokračo - Skautskom MO 2023 z8
V minulom roku bolo v našom skautskom oddiele o 30 chlapcov viac ako dievčat. Tento rok sa počet detí v oddiele zväčšil o 10%, pričom počet chlapcov sa zväčšil o 5% a počet dievčat sa zväčšil o 20%. Koľko detí máme tento rok v oddiele? - Odpočítajú 82333 Myslím si tri čísla, keď ich sčítam dostanem 16, keď od súčtu prvých dvoch čísel odpočítajú tretie dostanem 10, keď od súčtu prvého a tretieho čísla odčítajú druhé dostanem 8. Ktoré čísla si myslím?
- Štvoruholník 14
Daný je štvorec ABCD. Stred AB je E, stred BC je F, CD je G a stred DA je H. Spojíme AF, BG, CH a DE. Vo vnútri štvorca (približne v strede) priesečníky týchto úsečiek vytvoria štvoruholník. Vypočítajte obsah tohto štvoruholníka. Ďakujem - MO Z6-I-3 2022
Magda si vystrihla dva rovnaké rovnoramenné trojuholníky, z ktorých každý mal obvod 100 cm. Najprv z týchto trojuholníkov zložila štvoruholník tak, že ich k sebe priložila ramenami. Potom z nich zložila štvoruholník tak, že ich k sebe priložila základňami - Trojuholníka 81293
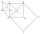Na obrázku sú znázornené štvorce ABCD, EFCA, CHCE a IJHE. Body S, B, F a G sú po rade stredy týchto štvorcov. Úsečka AC je dlhá 1 cm. Určite obsah trojuholníka IJS. Prosím pomôžte... - MO z9 2022
Sú dané dva zhodné rovnostranné trojuholníky ABC a BDE tak, že veľkosť uhla ABD je väčšia ako 120° a menšia ako 180° a body C, E ležia v rovnakej polrovine vymedzenej priamkou AD. Priesečník CD a AE je označený F. Určte veľkosť uhla AFD. - SKMO Z9 2022
Vrcholy štvorca ABCD spája lomená čiara DEFGHB. Menšie uhly pri vrcholoch E, F, G, H sú pravé a úsečky DE, EF, FG, GH, HB postupne merajú 6 cm, 4 cm, 4 cm, 1 cm, 2 cm. Určite obsah štvorca ABCD.
Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať. Riešenie príkladov z matematiky.
